Question 177194: find three consecutive integers such that the product of the two smaller inters is 2 more than ten times the largest integers.
Answer by EMStelley(208)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's call the smallest of the three integers x. Remember that consecutive means in order, such as 2,3,4. So we can call the next integer x+1 and the third one x+2. Then the "product of the two smaller integers" can be represented as 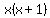 and "2 more than ten times the largest integer" can be represented as and "2 more than ten times the largest integer" can be represented as 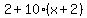 . So we have . So we have





So we get that x=11 and x=-2. How do we know which one is correct? Or maybe they are both correct? If x=11, the other two are x+1=12 and x+2=13. If x=-2, the other two are x+1=-1 and x+2=0. Let's check the answer with these solutions.
11(12)=2+10(13)
132=2+130
So x=11 is a solution.
-2(-1)=2+10(0)
2=2
So both x=11 and x=-2 are solutions. Thus, 11,12,13 and -2,-1,0 work.
|
|
|