Question 1203707: Find five consecutive integers such that:
“The sum of the first and 4 times the third is equal to 56 less than 3 times the sum of the second, fourth, and fifth.”
Found 3 solutions by josgarithmetic, MathLover1, ikleyn:
Answer by josgarithmetic(39709)   (Show Source): (Show Source):
Answer by MathLover1(20854)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The formula for a sequence of consecutive integers is  , ,  , ,  , ,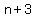 , , 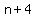 ,..., ,..., 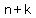 . .
The sum of the first and  times the third is equal to times the third is equal to  less than less than 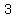 times the sum of the second, fourth, and fifth. times the sum of the second, fourth, and fifth.






five consecutive integers are: , ,  , ,  , ,  , , 
check:



Answer by ikleyn(53487)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find five consecutive integers such that:
“The sum of the first and 4 times the third is equal to 56 less than 3 times
the sum of the second, fourth, and fifth.”
~~~~~~~~~~~~~~~~
Let the numbers n, (n+1), (n+2), (n+3) and (n+4) be five consecutive integer numbers.
Write equation as you read the problem
n + 4*(n+2) = 3*((n+1) + (n+3) + (n+4)) - 56.
Simplify step by step
n + 4n + 8 = 3*(3n+8) - 56
5n + 8 = 9n + 24 - 56
8 - 24 + 56 = 9n - 5n
40 = 4n
n = 40/4 = 10.
ANSWER. The numbers are 10, 11, 12, 13, 14.
Solved.
|
|
|