SOLUTION: Find three consecutive even integers such that the square of the first is 80 less than the square of the third. (Only an algebraic solution will be accepted. )

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Find three consecutive even integers such that the square of the first is 80 less than the square of the third. (Only an algebraic solution will be accepted. )      Log On


   

Question 1102792: Find three consecutive even integers such that the square of the first is 80 less than the square of the third. (Only an algebraic solution will be accepted. )
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let n be the central of these tree consecutive integers, so that the numbers are

n-2, n and n+2.


Then the condition says

(n+2)^2 - (n-2)^2 = 80,   or, expanding parentheses,

n^2 + 4n + 4 - (n^2 -4n +4) = 80,

which is simplified to

8n = 80.


Hence, n = 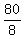80%2F8 = 10.


Answer.  The numbers are 8, 10 and 12.


Check.   12^2 - 8^2 = 144 - 64 = 80.   ! Correct !

Solved.