SOLUTION: Suppose one of the following numbers is chosen at random. 1 2 3 4 5 6 What is the probability the number chosen is even, given that it is greater than 2?

There are two ways to do it:

Method 1. Reduce the sample space to only what's given.

{1, 2, 3, 4, 5, 6}

The "given" part is "that it is greater than 2" 

So reduce the sample space by eliminating all elements
which do not satisfy the requirement "that it is 
greater than 2".  So we eliminate 1 and 2 from the
sample space, and so we now have the reduced sample 
space:

{3, 4, 5, 6}

Now answer the question asked with regard to only this 
reduced sample space:

>>...What is the probability the number chosen is even?..<<

There are only 2 even numbers, 4 and 6.

So that's 2 out of 4 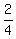or  or .

------------------------------------

Method 2.  By the formula

          P(A&B)
P(A|B) = --------
           P(B)

where A = "Number is even"
      B = "Number is greater than 2"

Then P(A&B) = P(even and greater than 2) = 
2 ways out of 6 =  = 

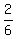and P(B) = P(greater than 2) = 4 ways out of 6 =
 = 

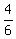P(A|B) =  =  =  =     

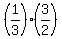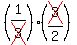Edwin