Question 1209959: A club buys tickets for 15 seats in a row for a local production and then sends the tickets randomly to the 15 people who ordered seats. Of these 15 people, 9 are actors and 6 are backstage workers. Find the probability that: a. An actor and backstage worker will receive tickets sitting together. b. The actors will be seated together, and the backstage workers will be seated together.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem into two parts:
**Understanding the Problem**
* We have 15 seats in a row.
* 9 people are actors (A).
* 6 people are backstage workers (B).
* Tickets are assigned randomly.
**a) Probability an Actor and Backstage Worker Sit Together**
1. **Calculate the total number of arrangements:**
The total number of ways to arrange the 15 people in the 15 seats is 15! (15 factorial).
2. **Calculate the number of arrangements where an actor and backstage worker sit together:**
This is more complex. We'll use the complementary probability: calculate the arrangements where *no* actor and backstage worker sit together, and subtract it from the total.
* **Consider pairs:**
An actor and backstage worker sit together as a pair (AB or BA).
* **Instead, calculate the probability that they are never together:**
This calculation is very complex.
* **Instead, a simpler approach is to use conditional probability:**
* **Probability of the first seat being an actor:** 9/15
* **Probability of the second seat being a backstage worker:** 6/14
* **Probability of the first seat being a backstage worker:** 6/15
* **Probability of the second seat being an actor:** 9/14
* **Probability that the first two are an actor and backstage worker:** (9/15)*(6/14) + (6/15)*(9/14) = 54/210 + 54/210 = 108/210
* **However, this only works for the first two seats. It is far more complicated to calculate for all seats.**
* **Instead, we will use a simpler approach of approximation:**
* Consider the number of pairs of seats. There are 14 pairs of adjacent seats.
* The probability that any specific pair has an actor and backstage worker is approximately (9/15)(6/14) + (6/15)(9/14) = 108/210 = 18/35.
* The probability that *at least one* pair has an actor and backstage worker is difficult to calculate precisely.
* However, the probability that a specific pair has an actor and backstage worker is 18/35, so it is likely that they will sit together.
**b) Probability Actors Sit Together and Backstage Workers Sit Together**
1. **Treat actors as a single block:**
Consider the 9 actors as one block (A) and the 6 backstage workers as another block (B).
2. **Arrange the blocks:**
There are 2! (2 factorial) ways to arrange these two blocks (AB or BA).
3. **Arrange the actors:**
There are 9! ways to arrange the 9 actors within their block.
4. **Arrange the backstage workers:**
There are 6! ways to arrange the 6 backstage workers within their block.
5. **Calculate the number of favorable arrangements:**
The number of favorable arrangements is 2! * 9! * 6!
6. **Calculate the total number of arrangements:**
The total number of arrangements is 15!
7. **Calculate the probability:**
Probability = (2! * 9! * 6!) / 15!
8. **Simplify:**
Probability = (2 * 9! * 6!) / 15! = (2 * 6!) / (15 * 14 * 13 * 12 * 11 * 10) = (2 * 720) / 3603600 = 1440/3603600 = 1/2502.5
Probability = 1440/3603600 = 4/10010
**Answers**
* **a) Probability an actor and backstage worker sit together:** This is a complex calculation and requires more advanced methods. It is likely a high probability.
* **b) Probability actors and backstage workers sit together:** 4/10010 or approximately 0.0003996.
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A club buys tickets for 15 seats in a row for a local production and then sends the tickets randomly
to the 15 people who ordered seats. Of these 15 people, 9 are actors and 6 are backstage workers.
Find the probability that:
(a) An actor and backstage worker will receive tickets sitting together.
(b) The actors will be seated together, and the backstage workers will be seated together.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
- - - - - To me, this problem and this case are EXCEPTIONALLY INTERESTING. - - - - - - -
- - - - - - - - - - - - - - - - - - Below I will explain WHY. - - - - - - - - - - - - - - - - - - - - - - - -
Question (a), if to read it literally as it is written in the post, asks to find
the probability that some of 9 actors sits next to some of 6 backstage workers.
The answer is OBVIOUS: this probability is 100%.
Indeed, having 15 seats in a row, 9 actors and 6 backstage workers, it is IMPOSSIBLE to place
them in a way that no actor sits next to some backstage worker.
The answer is at the level of common sense and at the level accessible to a kindergarten child.
@CPhill, which is a synonym to Artificial Intelligence, in his post starts create
irrelevant reasoning and CAN NOT produce right answer.
From it, I conclude that this AI is not able to make
OBVIOUS elementary basic logical implications, at all.
For me, it is 100% proof that this concrete AI, at its stage of development,
is not able to think, at all, and does not possess elementary common sense
even of the level of a kindergarten child.
It is WHY this case and this post by @CPhill are interesting to me.
It is why this case should be interesting to you, my reader.
- - - - - - - - Now I will return to the problem itself - - - - - - - -
- - - - - - - - - - - - - - - - Part (a) - - - - - - - - - - - - - - - -
I don't know, WHY question (a) in this post is posed this way.
It may be a Math joke. It may be a TRAP.
It may be, that the author/(the creator or the visitor) was intended to ask what is the probability
that some PARTICULAR actor A will sit next to some PARTICULAR backstage worker B.
If so, then the solution is as follows:
Then we consider this pair (A,B) as one unit, and we have then 14 possible positions for this unit
in the row of 15 seats. We also have 15! permutations for 15 persons, in all,
and 2 possible permutations inside the pair (A,B).
Therefore, the probability that particular A and particular B sit together is
P = 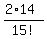 = = 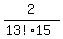 = = 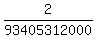 = 2.14121E-11. = 2.14121E-11.
- - - - - - - - - - - - - - - - Part (b) - - - - - - - - - - - - - - - -
Question (b) asks to find the probability that the actors seat together, and the backstage workers seat together.
Then we have a compact group of 9 actors with 9! permutations inside this group,
and a compact group of 6 backstage workers with 6! permutations inside this group.
The answer to question (b) is
P =  = = 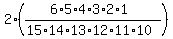 = =  = 0.0003996.
The factor ' 2 ' in the numerator is to account for two different possible placements
of the group of actors and the group of backstage workers. = 0.0003996.
The factor ' 2 ' in the numerator is to account for two different possible placements
of the group of actors and the group of backstage workers.
Solved.
/////////////////////////////////////
This problem, in its part (a), was a crucial TEST for the AI,
and the AI  this test. this test.
---------------------------------
This story has interesting continuation.
On September 2, 2025, I posted this problem to the Google AI, again.
This time, it produced correct, perfect and ideal solution.
Thanks to god, this AI is able to learn from the Internet.
It shows how it is important for this AI to have an adequate qualified tutor/teacher/mentor.
|
|
|