Question 1167219: A scholarship committee has $3000 to award this year and has 12 qualified candidates. Fran thinks that individual awards of $1500, $1000, and $500 would be appropriate, while Pat thinks that 3 awards of $1000 each would seem logical. Answer the following questions.
a) Count the number of possible outcomes for each plan.
b) Explain which plan would allow the scholarship committee to reach a consensus most quickly.
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
A scholarship committee has $3000 to award this year and has 12 qualified candidates.
Fran thinks that individual awards of $1500, $1000, and $500 would be appropriate,
while Pat thinks that 3 awards of $1000 each would seem logical. Answer the following questions.
a) Count the number of possible outcomes for each plan.
b) Explain which plan would allow the scholarship committee to reach a consensus most quickly.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
If we consider Fran's plan, then the number of all different possible and distinguishable triples
is the product 12*11*10 = 1320 of three integer numbers starting from 12 in the descending order.
It is so, because the order inside each such triple does matter:
for example, triple (Alex, Berta, Carl) is different from triple (Berta, Alex, Carl),
because the participants obtain different awards.
If we consider Pat's plan, then the number of all different possible and distinguishable triples
is the number of combinations  =  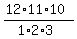=  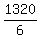= 220 of three participants
taken at a time from 12 participants.
It is so, because the order inside each such triple does NOT matter:
for example, triple (Alex, Berta, Carl) is not distinguishable from triple (Berta, Alex, Carl),
because the participants obtain the same awards.
Thus part (a) is solved completely and question (a) is answered, in full.
It is a good question and a good problem, because it teaches you
to distinct between permutations and combinations, depending on context.
Regarding question (b), I do not understand its meaning.
May be, the most fair/equitable way is to distribute all $3000 equally between all 12 participants ?
May be, the most fair way is to award with $3000 the most qualified candidate ?
I don't know which way is better.
Flip a coin. Or declare a war - on your choice.
To speak seriously, the way how this question (b) is posed in the post is not a mathematical.
In my view, it would be much better to exclude question (b) from the problem, at all.
Why ? - - - Because there is no room for nonsense in Math problems.
If you remove this question from the post, then the problem will become ideal from the educative point of view.
|
|
|
