Question 1160672: The times a teacher takes to grade one page of an exam are normally distributed with a mean of 4 minutes and a standard deviation of 1 minute. For about what percent of exams does a teacher grade one page in less than 7 minutes?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
The times a teacher takes to grade one page of an exam are normally distributed with a mean of 4 minutes
and a standard deviation of 1 minute. For about what percent of exams does a teacher grade one page
in less than 7 minutes?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that in this problem 7 minutes time interval is 3 minutes greater than 4 minutes, the average time.
So, apply the empirical rule for normal distribution, which says that 99.7% of data fall into three
standard deviations from the mean.
Using this rule, we account 50% for checking exams faster than 4 minutes, and add to it
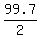 = 49.85% for the exams to check them from 4 minutes to 7 minutes.
Thus the answer to the question is 50% + 49.85% = 99.85%. <<<---=== ANSWER
At this point, the problem is solved completely.
///////////////////////////////////////////////
By the way, out of curiosity, I submitted this problem to Google AI today (07/14/2025).
It produced wrong solution, saying that the answer is 99.7%.
So, although the problem is very simple, AI could not solve it correctly - - - and failed.
It is because this version AI, actually, can not think, in usual meaning of this word.
It only can re-write a prototype of a solution from a template
in its base of knowledge, if it will find an appropriate template there.
But in this case, it could not find an appropriate template - - - and failed.
It is what I always say about the current version of AI in solving school Math problems:
- it works perfectly, if it finds a template with a correct solution to re-write from.
If it will not find such a template - it fails.
Naturally, I informed Google AI about their fault in this problem via their feedback system
and provided the link to this correct solution. So, from now this Google AI is a bit smarter than it was before.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Next day, 07/15/25, I checked Google AI by posting this problem again.
This time, it created a correct solution, so I am satisfied now.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a different method than shown by the other tutor for doing the calculations.
The basic rule is that 99.7% of scores in a normal distribution are within 3 standard deviations of the mean. That means 0.3% of the scores are more than 3 standard deviations from the mean.
That 0.3% is equally split between the scores that are more than 3 standard deviations above the mean and the ones that are more than 3 standard deviations below the mean, so 0.15% of the scores are more than 3 standard deviations above the mean.
And that means that the percentage of scores that are less than 3 standard deviations above the mean is 100 - 0.15 = 99.85.
ANSWER: 99.85%
|
|
|
