SOLUTION: Two unbiased dice are thrown in the air. Find the probability that the sum of the scores is either perfect or a prime number.

Here are all 36 possible rolls. Each sum occurs
on the diagonals that slant this way /:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

 P(2)=1/36
 P(3)=2/36
 P(4)=3/36
 P(5)=4/36
 P(6)=5/36
 P(7)=6/36
 P(8)=5/36
 P(9)=4/36
P(10)=3/36
P(11)=2/36
P(12)=1/36 

A perfect number is one equal to the sum of its divisors other 
than itself. The divisors of 6 other that 6 are 1,2, and 3 and 
1+2+3=6.

[The next perfect number is 28 = 1+2+4+7+14, so 6 is the only
perfect number obtainable by throwing two dice.]

2,3,5,7,11 are the primes that can be thrown.

P(perfect or prime) = P(6)+P(2)+P(3)+P(5)+P(7)+P(11) =  =  = 

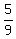Edwin