SOLUTION: a pair of dice are tossed twice . what is the probability of getting a total of 7 & 11?

There are 6 ways to roll 7: 

(1,6) (2,5) (3,4) (4,3) (5,2) (6.1).

There are 2 ways to get 11: 

(6,5) (5,6).

There are 36 ways to roll a pair of dice:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)  

The probablity of rolling a 7 is  or .

The probablity of rolling a 11 is  or .

--------------------

Not being a craps shooter, I am ignorant of the rules of the game J.

So I don't know whether we must get a 7 first and an 11 second,
or whether it will be acceptable to get an 11 first and a 7 second.
So I'll do it both eway.

(a) assuming we MUST get 7 first and 11 second:

P(7 first AND 11 second) = P(7 first) × P(11 second) =  = 

---------------------------------


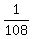(b) assuming we can get 7 first and 11 second OR get 11 first and 7 second:

P(7 first AND 11 second) OR (11 first AND 7 second) = 

P(7 first) × P(11 second) + P(11 first)×P(7 second) = 
 =  =  = 

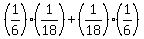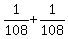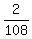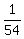Edwin