Question 888698: Can someone help with the following:
In her first year of university, Mary received the following grades:
12, 8, 12, 11, 9, 6
Similarly in his first year, Bob received the following grades:
5, 9, 9, 6, 5, 7
Compute the population mean and variance for both.
My Work:
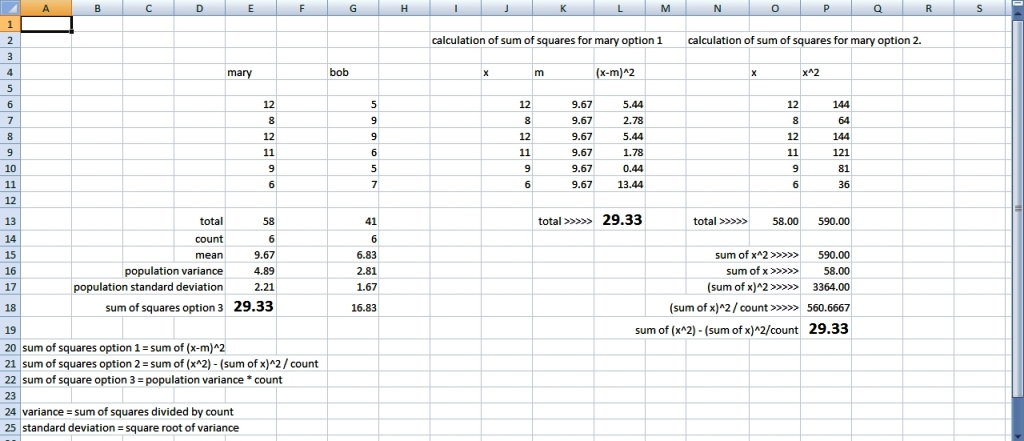
Mary's mean 9.67
Bob's mean 6.83
not sure of the variance
thanks Paul
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sum of squares for mary is 29.33
sum of squares for bob is 16.83
the population variance for mary is 4.89
the population variance for bob is 2.81
the population variance is equal to the sum of squares divided by the count of the number of items.
for mary, this would be 29.33 / 6 = 4.89
for bob, this would be 16.83 / 6 = 2.81
the sum of squares can be calculated in two basic ways.
first way is:
sum of squares = sum of (x-m)^2, where x is the individual data values and m is the mean of the data set.
second way is:
sum of squares = sum of (x^2) - (sum of x)^2 / n, where x is the individual data values and n is the count of data items.
both these methods are shown in the excel spreadsheet under sum of squares option 1 and sum of squares option 2.
sum of squares option 3 is equal to the population variance * the count of items.
this can be done in excel because excel provides a formula for variance and a formula for count but does not provide a direct formula for sum of squares, so you can get the sum of squares through excel by multiplying the population variation by the count of items.
the calculations are shown in the following picture of an excel spreadsheet.
|
|
|