Question 872884: Seven single digit numbers have a median of 6 and a range of eight. The mode of the seven numbers is 3. Find the seven numbers
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The median is a value such that as many numbers are less than the median, as are more than the median.
If the median of 7 numbers is  , because 7 is an odd number,
it means  is one of the numbers, appearing an odd number of times (1, 3, 5, or 7 times),
and from the other numbers that are not (if any),
half of them are less than 6,
and the other half of the remaining numbers are more than 6.
The mode is the most frequent value. So at least two of the numbers must be  .
The range is the difference between the greatest and the smallest values.
If zero was considered a "single digit number", it could be the smallest of the 7 numbers, and 8 would be the greatest.
If zero is not one of the 7 numbers, the smallest must be  and the greatest would be  .
If the smallest number is 0, the greatest is 8, and if the smallest number is 1, the greatest is 9.
Larger numbers cannot be the smallest of all the 7 numbers, because if  is the smallest, with a range of  , then
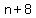 would be the greatest of the numbers,
and for it to be a "single digit number," it must be
 <--> .
So, 0 or 1 is one of the numbers, and that smallest number (0 or 1),
along with  (appearing twice),
accounts for the 3 numbers smaller than .
That takes care of the 4 smallest numbers.
In decreasing order, we have , , , and then 1 or 0.
Since is the median, and is the mode and appears twice, we need 3 different numbers greater than to complete our set.
The only possible answer is  , , and  .
Since is the greatest of the numbers, and the range is 8, then the smallest number is  .
So the 7 numbers are  .
|
|
|
