Question 843064: If you have 3 number cubes, what is the probability that you will roll three of a kind or a sum that is an odd number?
I have tried to solve this problem but I don't understand how to figure out the probability of rolling 3 of a kind.
Found 3 solutions by richard1234, Fombitz, Theo:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three-of-a-kinds: (1,1,1), (2,2,2), ..., (6,6,6) out of 216 possibilities total, so the probability of a three-of-kind is 6/216 = 1/36.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Look at all of the possible outcomes.
111
112
113
.
.
.
665
666
There are  or or 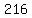 of them. of them.
Three of a kind outcomes are {111,222,333,444,555,666}.
There are 6 of those.

.
.
.
When you sum the numbers, half of the 216 sum to even, half sum to odd.

So to sum the probability of 3 of a kind or sum that's odd, add the probabilities. Remember to remove the 3 of a kind sums that are odd (111,333,555) so you don't count those twice (3/216 outcomes).

Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the probability of getting three of a kind of the sum of the three cubes is an odd number is equal to:
the probability of getting three of a kind
plus the probability of getting the sum of the cubes equal to an odd number
minus the probability of getting three of a kind and the sum of the cubes is equal to an odd number.
the probability of getting three of a kind is equal to:
1/6 * 1/6 * 1/6 * 6 which is equal to:
6/216
out of the 6, 3 of them will have a sum that is odd (numbers 1,3,5) and 3 of them will have a sum that is even (numbers 2,4,6).
we need to subtract the ones that have an odd sum because they will otherwise be double counted.
you get:
6/216 minus 3/216 which is equal to:
3/216
the net probability of getting 3 of a kind whose sum is odd is therefore equal to 3/216. *****
the probability of the sum of the three cubes having a sum that is odd is broken up into 2 parts.
the first part is the probability that each of the cubes is odd.
this will result in a sum that is odd.
the probability that each cube is odd is equal to 3/6.
the probability that all 3 cubes are odd is therefore equal to 3/6 * 3/6 * 3/6 which is equal to 27/216. *****
note that the probability that each cube is odd includes the cubes that are all the same (cubes with all 1's, cubes with all 3's, cubes with all 5's).
if we had not subtracted them from the total, they would have been double counted.
the subtraction was done above.
the only other way that the sum of the 3 cubes could be odd is that 2 of the cubes are even and the third cube is odd.
the probability of a cube being even is 3/6.
the probability of a cube being odd is 3/6.
the odd number are 1,3,5
the even numbers are 2,4,6
the probability of 2 of the cubes being even and 1 of the cubes being odd is therefore equal to 3 * 3/6 * 3/6 * 3/6 = 81/216 *****
the 3/6 * 3/6 * 3/6 is only one arrangement.
there are three arrangements of 2 even cubes and 1 odd cube.
those arrangements are:
even even odd
even odd even
odd even even
that's why the 3/6 * 3/6 * 3/6 was also multiplied by 3.
this takes care of the 3 possible arrangements.
the total probability is the sum of all 3 of these probabilities.
that will be 3/216 + 27/216 + 81/216.
the sum of all of that is equal to 111/216.
that's your answer is i did this correctly.
i verified with a much simpler example that the method is good so i'm reasonably confident the answer is good.
the formula for p(a or b) is:
p(a or b) = p(a) + p(b) - p(ab)
p(ab) is the probability of both occurring at the same time.
in this problem that was the probability that all cubes had the same number and that the sum was odd.
p(ab) in this problem was 3/216 which i subtracted from 6/216 up front.
if i had followed the script exactly, the end total would have been:
6/216 + 27/216 + 81/216 - 3/216.
the end result would have been the same with a total probability of 114/216 - 3/216 which would have been equal to 111/216.
|
|
|