Question 815320: 1. A ball is drawn at random from a box containing 6 red balls, 4 white balls, and 5 blue balls.
Determine the probability that the ball drawn is (a) red. (b) white, (c) not red. and (d) red or white.
2. In a certain high school class, consisting of 60 girls and 40 boys, it is observed that 24 girls and 16 boys wear eye glasses, if a student is picked at random from this class. What is the probability that student picked at random is a boy, what is the probability that a student wears eye glasses?
3. In a population of 3000 children under 5 , those with malnutrition is 31%, if 5 children are selected randomly what is the probability of:
a) 3 children with malnutrition
b) At more 2 are malnourished.
4. In a sample of 64 students given an examination in statistics, it is found that the mean weight is 57 kg with standard deviation 9 kg. Find :
i) The proportion of students weight 48-62 kg.
ii) The proportion of those less than 72 kg.
iii) The proportion of those less than 50 kg ?
iv) If the highest 5% of are over-weight, what is the Minimum score for an over-weight.
5. The mean weight of 500 male students at a certain college is 151 pounds (lb), and the standard deviation is 15 lb. Assuming that the weights are normally distributed, find the probability of students weight
(a) between 121 and 155 lb
(b) more than 185 lb.
c) if 4% of the students are overweight, what is the minimum weight to classify student as over weight?
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. A ball is drawn at random from a box containing 6 red balls, 4 white balls, and 5 blue balls.
Determine the probability that the ball drawn is
(a) red.
6 ways out of 15 =  = = 
(b) white,
4 ways out of 15 = 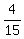
(c) not red.
That's the complement of (a), so it's 1 -  = = 
(d) red or white.
10 ways out of 15 =  = =  ---------------------------------------------------
---------------------------------------------------
5. The mean weight of 500 male students at a certain college is 151 pounds (lb), and the standard deviation is 15 lb. Assuming that the weights are normally distributed, find the probability of students weight
(a) between 121 and 155 lb
TI-83 or 84 calculator under 2ND VARS
normalcdf(121,155,151,15)
.58238697
(b) more than 185 lb.
normalcdf(185,99999999,151,15)
.0117052622
(c) if 4% of the students are overweight, what is the minimum weight to classify student as over weight?
invNorm(1-.04,151,15)
177.2602911
Edwin
|
|
|