SOLUTION: How many different 6-player starting squads can be formed from a volleyball team of 11 players?

How many different 6-player starting squads can be formed from a volleyball
team of 11 players?

Let's say the 11 players are A,B,C,D,E,F,G,H,I,J,K

First we figure how many ORDERED groups (permutations) of 5 players there are,
where one such ORDERED group would be. say,

G,H,B,A,J,F

We could have chosen the first one (where the G is) any of 11 ways.

Then we could have chosen the second one (where the H is) any of the remaining
10 ways. That's (11)(10) ways.

Then we could have chosen the third one (where the B is) any of the remaining 9
ways. That's (11)(10)(9) ways.

Then we could have chosen the fourth one (where the A is) any of the remaining
8 ways. That's (11)(10)(9)(8) ways.

Then we could have chosen the fifth one (where the J is) any of the remaining 7
ways. That's (11)(10)(9)(8)(7) ways.

Then we could have chosen the sixth one (where the F is) any of the remaining 6
ways. That's (11)(10)(9)(8)(7)(6) ways. 

That would be the answer if they had to be in a certain order.

However we know that they don't have to be in any certain order. For example,
the ordered group G,H,B,A,J,F is not really a different group from the ordered
groups A,G,F,J,H,B or J,B,A,G,F,H or any other arrangement of those 6 players. 

So therefore

(11)(10)(9)(8)(7)(6) is entirely too large a number. Let's look at the sample
ordered group G,H,B,A,J,F to see how many times it is counted among the

(11)(10)(9)(8)(7)(6), so we can divide by that number.  

We could have chosen the first one (where the G is) any of 6 ways.

Then we could have chosen the second one (where the H is) any of the remaining
5 ways. That's (6)(5) ways.

Then we could have chosen the third one (where the B is) any of the remaining 4
ways. That's (6)(5)(4) ways.

Then we could have chosen the fourth one (where the A is) any of the remaining
3 ways. That's (6)(5)(4)(3) ways.

Then we could have chosen the fifth one (where the J is) any of the remaining 2
ways. That's (6)(5)(3)(2)(1) ways.

Then we could have chosen the sixth one (where the F is) ONLY the remaining 1
way. That's (6)(5)(4)(3)(2)(1) ways.

Since every group of 6 is counted among the (11)(10)(9)(8)(7)(6) ORDERED groups
(6)(5)(4)(3)(2)(1) times, the desired number is 

    
  
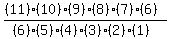Then you can have a good time canceling the factors of the denominator
into the factors of the numerator and end up with 462.

The answer could have been done as C(11,6) and the formula

 used as

 =



Edwin