Question 757712: Please help me with this question.
The CEO of a software company is committed to expanding the proportion of highly qualified women in the organizationís staff of salespersons. He believes that the proportion of women in similar sales positions across the country is less than 45%. Hoping to find support for his belief, he directs you to test
H0: p .45 vs H1: p < .45.
In doing so, you collect a random sample of 50 salespersons employed by his company, which is thought to be representative of sales staffs of competing organizations in the industry. The collected random sample of size 50 showed that only 18 were women.
What is the smallest level of significance at which you could reject the null in favor of the alternative hypothesis? Place your answer, rounded to 4 decimal places, in the blank. For example, 0.1234 would be a legitimate entry.
Answer by reviewermath(1029)   (Show Source): (Show Source):
You can put this solution on YOUR website! Q:
The CEO of a software company is committed to expanding the proportion of highly qualified women in the organizationís staff of salespersons. He believes that the proportion of women in similar sales positions across the country is less than 45%. Hoping to find support for his belief, he directs you to test
H0: p .45 vs H1: p < .45.
In doing so, you collect a random sample of 50 salespersons employed by his company, which is thought to be representative of sales staffs of competing organizations in the industry. The collected random sample of size 50 showed that only 18 were women.
What is the smallest level of significance at which you could reject the null in favor of the alternative hypothesis? Place your answer, rounded to 4 decimal places, in the blank. For example, 0.1234 would be a legitimate entry.
-----------------------------------------------------------------------
A:
Test Statistic,z = 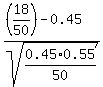 = -1.2792 = -1.2792
P-Value = P(Z < -1.2792) = normsdist(-1.2792) ≈ 
The answer is 0.1005 because we roundup.
|
|
|