SOLUTION: A box contains 2 red and 3 green balls.one ball is drawn from the box and replaced before another is drawn.what is the propability that at least one is red?

Algebra ->  Probability-and-statistics -> SOLUTION: A box contains 2 red and 3 green balls.one ball is drawn from the box and replaced before another is drawn.what is the propability that at least one is red?      Log On


   

Question 741742: A box contains 2 red and 3 green balls.one ball is drawn from the box and replaced before another is drawn.what is the propability that at least one is red?
Found 2 solutions by lynnlo, ikleyn:
Answer by lynnlo(4176) About Me  (Show Source):
Answer by ikleyn(53107) About Me  (Show Source):
You can put this solution on YOUR website!
.
A box contains 2 red and 3 green balls. One ball is drawn from the box and replaced before another is drawn.
What is the probability that at least one is red?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

The probability that at least one ball of the two is red is the sum

    P(1st is red, 2nd is green) + P(1st is green, 2nd is red) + P(both are red).


So, calculating this three-terms sum is one approach to solve the problem.


But there is another approach, more effective and less computationally consuming.


It is to calculate the probability "at least one ball is red" as the complement to the probability 
"both balls are green".


So, let calculate the probability that "both balls are green".  It is

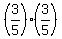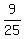    P(both balls are green) = %283%2F5%29%2A%283%2F5%29 = 9%2F25.


Hence, 

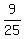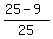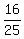    P(at least one ball is red) = 1 - P(both balls are green) = 1 - 9%2F25 = %2825-9%29%2F25 = 16%2F25.


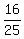ANSWER.  The probability that at least one ball is red is  16%2F25.

Solved.