SOLUTION: Five evenly matched horses (Applefarm, Bandy, Cash, Deadbeat, and Egglegs) run in a race. a. In how many ways can the first-, second-, and third-place horses be determined? b. Fi

Algebra ->  Probability-and-statistics -> SOLUTION: Five evenly matched horses (Applefarm, Bandy, Cash, Deadbeat, and Egglegs) run in a race. a. In how many ways can the first-, second-, and third-place horses be determined? b. Fi      Log On


   

Question 730309: Five evenly matched horses (Applefarm, Bandy, Cash, Deadbeat, and Egglegs) run in a race.
a. In how many ways can the first-, second-, and third-place horses be determined?
b. Find the probability that Deadbeat finishes first and Bandy finishes second in the race.
c. Find the probability that the first-, second-, and third-place horses are Deadbeat, Egglegs, and Cash, in that order.
Thanks!
Found 2 solutions by lynnlo, ikleyn:
Answer by lynnlo(4176) About Me  (Show Source):
Answer by ikleyn(53419) About Me  (Show Source):
You can put this solution on YOUR website!
.
Five evenly matched horses (Applefarm, Bandy, Cash, Deadbeat, and Egglegs) run in a race.
(a) In how many ways can the first-, second-, and third-place horses be determined?
(b) Find the probability that Deadbeat finishes first and Bandy finishes second in the race.
(c) Find the probability that the first-, second-, and third-place horses are Deadbeat, Egglegs, and Cash, in that order.
~~~~~~~~~~~~~~~~~~~~~~~~~ 

(a)  In 5*4*3 = 60 different ways.  This is  5P3 permutations.


(b)  P = %281%2F5%29%2A%281%2F4%29 = 1%2F20 = 0.05 = 5%.    


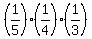(c)  P = %281%2F5%29%2A%281%2F4%29%2A%281%2F3%29 = 1%2F60.

Solved.

The formulas are self-explanatory.