SOLUTION: If a die is rolled 35 times, there are 6^35 different sequences possible. The following question asks how many of these sequences satisfies certain conditions. HINT [Use the decisi

Algebra ->  Probability-and-statistics -> SOLUTION: If a die is rolled 35 times, there are 6^35 different sequences possible. The following question asks how many of these sequences satisfies certain conditions. HINT [Use the decisi      Log On


   

Question 730135: If a die is rolled 35 times, there are 6^35 different sequences possible. The following question asks how many of these sequences satisfies certain conditions. HINT [Use the decision algorithm]

What fraction of these sequences have exactly 10 numbers less than or equal to 2? (Round your answer to four decimal places.)
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
That's the same as the binomial probability of getting exactly x=10 successes
out of n=35 trials with a probability of 1 success in 1 trial being p=1%2F3. 

The p=1%2F3 probability comes from the fact that there are 2 rolls, "1" and "2",
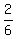out of the 6 possible rolls that are less than or equal to 2, and 2%2F6 reduces to 1%2F3.      

The formula for the binomial probability of getting exactly x successes
in n trials with a probability of p of 1 success in 1 trial is:

C(n,x)px(1-p)n-x

Our case is n=35, x=10, p=1%2F3.

Substituting those gives 0.1231203703

Rounding to four decimal places: 0.1231

Edwin