Question 698094: The probability that an electrical fuse coming off a production line is defective is 0.04 , Assuming that whether or not a fuse is defective is independent of whether or not any other fuse is defective , calculate the following probabilities to 3 significant figure (1) the probability that out of 30 fuses tested at least two will be defective
(2)the probability that the first fuse found to be defictive during any day will be the eleventh fuse tested
thanks
Answer by Positive_EV(69)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) This is a binomial distribution, with n = 30 fuses, and p = .04 that a fuse is defective. The probability mass function of the binomial distribution is
 , where n is the total number of trials, p is the probability of a success, and k is the number of successes in the trials. nCk refers to the total number of combinations of k objects drawn from n and equals , where n is the total number of trials, p is the probability of a success, and k is the number of successes in the trials. nCk refers to the total number of combinations of k objects drawn from n and equals 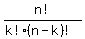 . For the purposes of this problem, ironically a "success" is the event that a fuse is defective. . For the purposes of this problem, ironically a "success" is the event that a fuse is defective.
The probability that at least two fuses are defective is a pain to calculate on its own. However, the compliment to the event that at least two fuses are defective is the event that 0 or 1 fuse is defective, which is much easier to calculate. A complimentary event has a probability equal to 1 - P(original event). The plan is thus to find P(0 or 1 defective), then subtract this value from 1.


The probability that 0 or 1 fuse is defective is .29386 + .36732 = .66118. The probability of the complimentary event, that 2 or more fuses are defective, is equal to 1 - .66118 = .33882, or .339 to 3 significant figures.
2) Since the events are independent, the probability that the first fuse to be defective is fuse 11 is equal to the probability that fuses 1-10 are working times the probability that fuse 11 is defective. The probability that fuses 1-10 all work is the probability that fuse 1 works times the probability that fuse 2 works times ... times the probability that fuse 10 works, which is (.96)^10 = .66483. The probability that the 11th fuse is defective is .04 regardless of what the first ten fuses do because the events are independent. Thus, the probability that the 11th fuse is the first defective one is the product of the probabilities that fuses 1-10 are all good times the probability that fuse 11 is defective = (.66483)*(.04) = .02659, or .0266 to 3 significant figures.
|
|
|