En español:
Diez personas al azar están sentadas en una mesa redonda. ¿Lo que la probabilidad p que dos miembros de una pareja en particular están sentados juntos?
Tenemos cosas de 9, 8 personas solteras y 1 par.
Supongamos que los dos
Ya que es una mesa redonda, estos 9 se consideran al mismo tiempo,
así que vamos a calcular la probabilidad de CDEFGHIJ (AB) y dividir
por 9.
(AB)CDEFGHIJ
C(AB)DEFGHIJ
CD(AB)EFGHIJ
CDE(AB)FGHIJ
CDEF(AB)GHIJ
CDEFG(AB)HIJ
CDEFGH(AB)IJ
CDEFGHI(AB)J
CDEFGHIJ(AB)
Hay 2! maneras de organizar el (AB) y 8! maneras de organizar la
CDEFGHIJ, por lo tanto, 2! ·8! = 2·40320 = 80640 maneras.
Luego dividimos por 9 ya que es una mesa redonda:
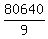 = 8960
-----------------------
= 8960
-----------------------
In English:
Ten people are randomly seated at a round table. What the probability p that two members of a couple in particular are sitting together?
We have 9 things, 8 single people and 1 couple.
Suppose the two
Since it is a round table, these 9 are considered all the same,
so we will calculate the probability of (AB)CDEFGHIJ and divide
by 9.
(AB)CDEFGHIJ
C(AB)DEFGHIJ
CD(AB)EFGHIJ
CDE(AB)FGHIJ
CDEF(AB)GHIJ
CDEFG(AB)HIJ
CDEFGH(AB)IJ
CDEFGHI(AB)J
CDEFGHIJ(AB)
There are 2! ways to arrange the (AB) and 8! ways to arrange the
CDEFGHIJ, therefore, 2!·8! = 2·40320 = 80640 ways.
Then we divide by 9 since it is a round table:
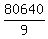 = 8960
Edwin
= 8960
Edwin