You will either get 0 jacks, 1 jack, 2 jacks, 3 jacks, or 4 jacks.
Calculate the probabilities of each of the 5 possibilities.
P(0 jacks)
There are 48 non-jacks. so we can choose them C(48,4) ways.
The denominator is C(52,4) So the probability is 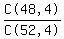 = 0.718737
P(1 jack)
We can choose the jack any of C(4,1) ways, we can choose the
3 non-jacks any of C(48,3) ways.
The denominator is C(52,4) So the probability is
= 0.718737
P(1 jack)
We can choose the jack any of C(4,1) ways, we can choose the
3 non-jacks any of C(48,3) ways.
The denominator is C(52,4) So the probability is  = 0.255551
P(2 jacks)
We can choose the 2 jacks any of C(4,2) ways, we can choose the
2 non-jacks any of C(48,2) ways.
The denominator is C(52,4) So the probability is
= 0.255551
P(2 jacks)
We can choose the 2 jacks any of C(4,2) ways, we can choose the
2 non-jacks any of C(48,2) ways.
The denominator is C(52,4) So the probability is  = 0.025000
P(3 jacks)
We can choose the 3 jacks any of C(4,3) ways, we can choose the
1 non-jack any of C(48,1) ways.
The denominator is C(52,4) So the probability is
= 0.025000
P(3 jacks)
We can choose the 3 jacks any of C(4,3) ways, we can choose the
1 non-jack any of C(48,1) ways.
The denominator is C(52,4) So the probability is  = 0.000709
P(4 jacks)
We can choose the 4 jacks any of C(4,4) ways.
The denominator is C(52,4) So the probability is
= 0.000709
P(4 jacks)
We can choose the 4 jacks any of C(4,4) ways.
The denominator is C(52,4) So the probability is 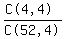 = 0.000004
Probability distribution:
X = the number of jacks:
X P(X)
0 0.718737
1 0.255551
2 0.025000
3 0.000710
4 0.000004
-------------
1.000002
The total of the probabilities would be 1 if
the probabilities weren't rounded off.
Edwin
= 0.000004
Probability distribution:
X = the number of jacks:
X P(X)
0 0.718737
1 0.255551
2 0.025000
3 0.000710
4 0.000004
-------------
1.000002
The total of the probabilities would be 1 if
the probabilities weren't rounded off.
Edwin