Question 643440: please help in solving this question :
Martin beats Jelena in 2 games out of 3 at tennis . what is the probability that jelena wins a set of tennis 6 games to 4 ?
tushar.langer@gmail.com
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website! >>Martin beats Jelena in 2 games out of 3 at tennis.<<
Therefore Jelena wins only 1 game out of 3 when playing agains Martin.
Therefore Jelena's probability of winning against Martin is  >>What is the probability that jelena wins a set of tennis 6 games to 4?<<
That's asking what is the probability that Jelena, playing aginst Martin,
will win 6 times and lose 4 times. That means she plays a total of 6+4 or
10 games and wins 6 out of the 10 games. [That's not very likely to happen,
since she usually loses to Martin, so we expect a very low probability]
That's the binomial probability of succeeding x=6 times out of n=10 trials,
with a probability of p=.
The binomial probability of succeeding x times out of n trials, with a
probability of p is given by the formula:
C(n,x)·px·(1-p)n-x
Substituting
C(10,6)· 6·(1-)10-6
C(10,6)·6·(1-)10-6
210· · 4
210··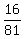
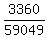
As a decimal 0.056901895 (round off as you were told).
You can also do it with a TI-83 or TI-84. You may have the
older model or the newer model. Either way,
Press 2ND VARS ALPHA MATH
-------------------------------------
If you have an older model press ENTER
You will see
binompdf(
Make it read
binompdf(10,1/3,
6)
press ENTER
you will see .056901895
-------------------------------------
If you have a newer model, you will see
trials:
p:
x value:
Paste
Make it read this way:
trials: 10
p:1/3
x value:6
Paste
Highlight Paste then press ENTER
You will see
binompdf(10,1/3,
6)
press ENTER
you will see .056901895
Edwin
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! this is a litle tricky, but the concept is as follows:
in order for jelena to win 6 games to 4, they both have to get to the point where jelena has won 5 games and martin has won 4.
that's a total of 9 games.
jelena then needs to win the 10th game.
since martin beats jelena 2 games out of 3, then:
the probability of martin winning any one game is 2/3.
the probability of jelena winning any one game is 1/3.
i will simplify the problem so you can see the concept and then i will apply the concept to your problem.
suppose you want jelena to win a set of 3 games by the score of 2 games to 1.
in order to that to happen, both jelena and martin will have had to have won 1 game apiece.
once that occurs, jelena then needs to win the third game.
consider the possible ways this can happen.
let j represent a game that is won by jelena
let m represnt a game that is won by martin.
the possible ways that we can get jelena and martin to win 1 game apiece is:
j m
m j
after we get to this point, jelena needs to win the third game to get:
j m j
m j j
now, since the probability jelena will win a game is 1/3 and the probability that martin will win a game is 2/3, then we can multiply by the probabilities to get the total probability of all 3 occurrences in each of the possible combinations above.
j m j becomes (1/3)*(2/3)*(1/3) = 2/27
m j j becomes (2/3)*(1/3)*(1/3) = 2/27
the total probability is the sum of these 2 possible combinations which then is equal to 4/27
in order to apply this concept to the larger numbers, we need some formulas.
the basic formula we will use is:
P(n,x) = C(n,x)*p^x*q^x
n represents the total number of games
x represents the number of games jelena needs to win.
p represents the probability jelena will win a game.
q represents the probability martin will win a game.
the probability of jelena winning 1 out of 2 games is given by the formula:
P(2,1) = C(2,1)*p^1*q^1
C is the combination formula of 2! / (1!*1!)
p is the probability of jelena winning a game = (1/3)
q is the probability of martin winning a game = (2/3)
P(2,1) means probability of winning 1 game out of 2.
that gets us to the 3d game which jelena has to win.
the formula becomes:
P(2,1)*p = C(2,1)*p^1*q^1*p
if i use this formula, i should get the same answer i got before which is that the total probability of jelena winning a set of 3 games by the score of 2 to 1 is equal to 4/27.
let's see if that works.
the formula becomes:
P(2,1)*p = C(2,1)*p^1*q^1*p
C(2,1) = 2!/(1!*1!) = 2
p^1 = (1/3)^1 = (1/3)
q^1 = (2/3)^1 = (2/3)
p = (1/3)
replace letters with appropriate numbers, we get:
P(2,1)*(1/3) = 2*(1/3)*(2/3)*(1/3) which becomes:
P(2,1)*(1/3) = 2*2/27 which becomes:
P(2,1)*(1/3) = 4/27.
it looks like the formula is good so we'll apply the same formula to your problem.
your problem is that jelena needs to win the set of 10 games by the score of 6 games to 4.
in order for that to happen, jelena needs to have won 5 games and martin needs to have won 4 games out of a total of 9 games and then jelena needs to win the 10th game.
the formula becomes:
P(9,5)*p = C(9,5)*p^5*q^4*p
C(9,5) = 9!/(5!*4!) = 126
p^5 = (1/3)^5 = (1/243)
q^5 = (2/3)^4 = (2^4)/(3^4) = 16/81
the formula becomes:
P(9,5)*(1/3) = C(9,5)*(1/3)^5*(2/3)^4*(1/3) which becomes:
P(9,5)*(1/3) = 126 * (1/243) * (16/81) * (1/3) which becomes:
P(9,5)*(1/3) = 126 * 16 / 59049 which becomes:
P(9,5)*(1/3) = 2016 / 59049
this can be simplified to 224 / 6561
in decimal form the answer is:
P(9,5)*(1/3) = .034141137
the complicating factor was the number of ways to get to the point where jelena has won 5 games and martin has won 4.
no matter how they do it, they both have to get to this point in order for jelena to win by 6 to 4.
the number of ways that can happen is C(9,5) = 9! / (5!*4!) = 126.
here's just a couple of ways that can happen:
j j j j j m m m m
m m m m j j j j j
m m j j j m m j j
j m j m j m j m j
each one of these ways has a probability associated with it which then has to be multiplied by (1/3) in order to include the probability of jelena winning the 10th game.
that's what the formula is designed to model.
if i did it correctly, your answer should be as indicated.
P(9,5)*(1/3) = .034141137 in decimal form and is equal to 224/6561 in fraction form.
|
|
|
