Question 638348: How do you write a linear equation from x and y coordinates
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1.
Find the slope of the line by dividing the change in y-coordinates by the change in x-coordinates:
 . .
For example, given the coordinates (2, 0) and (-1, 3), the  . .
If both of the x-coordinates equal some value  , the slope and y-intercept are undefined, and the equation for the line will be , the slope and y-intercept are undefined, and the equation for the line will be  . .
2.
Calculate the y-intercept by multiplying the slope times one of the x-coordinates and subtracting the product from the y-coordinate of the same point:
 , where , where 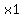 and and 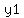 are coordinates of one of the given points. are coordinates of one of the given points.
For example, knowing that the  , use the point (2, 0): , use the point (2, 0):  . .
3.
Write the equation for the line in the 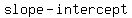 format: format:
 . .
In the given example,  . .
4.
Verify the equation by plugging in the  - and - and 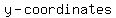 of the given points. If the equation remains balanced after simplifying, your equation is good. of the given points. If the equation remains balanced after simplifying, your equation is good.
For example, given the equation  , plug in the first point (2,0): , plug in the first point (2,0):
 . That's true, so everything checks out so far. . That's true, so everything checks out so far.
Try again with (-1, 3):
 . That's true too, so the equation is good. . That's true too, so the equation is good.
|
|
|