Question 636456: If a computer code contains 2 letters and 3 numbers and none can repeat, how many combinations are possible?
I am thinking:
26*25*24...*1*25 PLUS 9*8*7...*1*8*7. Would that be correct for the formula?
Thank you!
Jama
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your formula does not sound right. I cannot figure out how you derived it. My logic gives me different answers. (Disclaimer: I have been wrong at times)
I see two possible interpretations of the problem:
 a computer code/password is made up of two letters together, followed by 3 numbers, a computer code/password is made up of two letters together, followed by 3 numbers,
like  , ,
you have 26 choices for the first character.
For each of those 26 choices, you have 25 choices for the second character.
That gives you 26*25 choices for the two beginning characters (letters).
For each of those 26*25 choices, you have 10 choices for the third character.
That results in 26*25*10 choices for the first three characters.
For each of those 26*25*10 choices, you have 9 choices for the fourth character.
You end up with 26*25*10*9 choices for the first four characters.
For each of those 26*25*10*9 choices, you have 8 choices for the fifth character.
That gives you  choices overall. choices overall.
However,  the letters and numbers could be scrambled into any order, the letters and numbers could be scrambled into any order,
like  , or , or  , ,
there are more possibilities.
In that case, the 26*25 two letter codes, would be 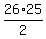 two-letter sets, two-letter sets,
because codes AB and BA use the same set {A, B}.
Similarly, the 10*9*8 three-digit codes represent  three three-digit sets. three three-digit sets.
Then, you would have 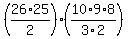 different sets made of 2 letters and three digits. different sets made of 2 letters and three digits.
Each set could be re-arranged 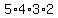 different ways, giving you different ways, giving you
 different codes. different codes.
|
|
|