Question 548416: Given that P(A) = 0.5, P (B) =0.3, and P(A and B) = 0.10, determine P(AlB)
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two ways to do it: (1) By formula and (2) By chart:
(1) By formula.
This is the easy way when you don't have complement event A' or
the complement event B'
P(A|B) = 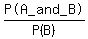 = =  = =  ---------------------------
However, you may have other problems with A' or with B'. If so the
chart method is better:
(2) By chart
P(A) = 0.5, P (B) =0.3, and P(A and B) = 0.10, determine P(AlB)
Make this probability chart:
| B | B' | Totals
===========================
A | | |
---------------------------
A' | | |
===========================
Totals| | |
Fill in the lower right cell total with probability 1.0, (for certainty).
Fill in the upper left cell with 0.1 because that cell is to contain
the probability of (A and B)
Fill in the total probability of A as 0.5
Fill in the total probability of B as 0.3
| B | B' | Totals
===========================
A | 0.1 | | 0.5
A' | | |
===========================
Totals| 0.3 | | 1.0
Fill in the probability for (A and B') by subtracting 0.1 from 0.5, getting 0.4
Fill in the probability for (A' and B) by subtracting 0.1 from 0.3, getting 0.2
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | |
===========================
Totals| 0.3 | | 1.0
Fill in the total probability for A' by subtracting 0.5 from 1.0, getting 0.5
Fill in the total probability for B' by subtracting 0.3 from 1.0, getting 0.7
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
Finally, fill in the probability for A' and B' by subtracting 0.4 from 0.7, getting 0.3. Notice that it automatically checks because the total of B'
is correctly 0.7:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
Now we can find any of the 8 possible conditional probabilities:
In particular, we want to find P(A given B), since B is given, we ignore everything except the B column, the numbers in red below:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
The desired conditional probability P(A|B) =
---------------------------
However, you may have other problems with A' or with B'. If so the
chart method is better:
(2) By chart
P(A) = 0.5, P (B) =0.3, and P(A and B) = 0.10, determine P(AlB)
Make this probability chart:
| B | B' | Totals
===========================
A | | |
---------------------------
A' | | |
===========================
Totals| | |
Fill in the lower right cell total with probability 1.0, (for certainty).
Fill in the upper left cell with 0.1 because that cell is to contain
the probability of (A and B)
Fill in the total probability of A as 0.5
Fill in the total probability of B as 0.3
| B | B' | Totals
===========================
A | 0.1 | | 0.5
A' | | |
===========================
Totals| 0.3 | | 1.0
Fill in the probability for (A and B') by subtracting 0.1 from 0.5, getting 0.4
Fill in the probability for (A' and B) by subtracting 0.1 from 0.3, getting 0.2
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | |
===========================
Totals| 0.3 | | 1.0
Fill in the total probability for A' by subtracting 0.5 from 1.0, getting 0.5
Fill in the total probability for B' by subtracting 0.3 from 1.0, getting 0.7
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
Finally, fill in the probability for A' and B' by subtracting 0.4 from 0.7, getting 0.3. Notice that it automatically checks because the total of B'
is correctly 0.7:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
Now we can find any of the 8 possible conditional probabilities:
In particular, we want to find P(A given B), since B is given, we ignore everything except the B column, the numbers in red below:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
The desired conditional probability P(A|B) =  = =  The advantage of the table method is that we can easily find all 8 possible
conditional probabilities, by ignoring everything except what is given, and
dividing the probability by the total in that column or row. For instance,
suppose we wanted to find
P(B|A).
We would ignore everything but the (given) A row
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
and divide the probability
for B in that row by the total probability of A, getting
The advantage of the table method is that we can easily find all 8 possible
conditional probabilities, by ignoring everything except what is given, and
dividing the probability by the total in that column or row. For instance,
suppose we wanted to find
P(B|A).
We would ignore everything but the (given) A row
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
and divide the probability
for B in that row by the total probability of A, getting 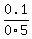 = =  .
All 8 of the conditional probabilities can be gotten from the table:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
P(A|B) = .
All 8 of the conditional probabilities can be gotten from the table:
| B | B' | Totals
===========================
A | 0.1 | 0.4 | 0.5
A' | 0.2 | 0.3 | 0.5
===========================
Totals| 0.3 | 0.7 | 1.0
P(A|B) =  = =  P(A|B') =
P(A|B') =  = =  P(A'|B) =
P(A'|B) = 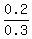 = =  P(A'|B') =
P(A'|B') = 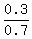 = = 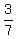 P(B|A) =
P(B|A) =  = =  P(B|A') =
P(B|A') = 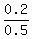 = =  P(B'|A) =
P(B'|A) = 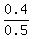 = = 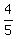 P(B'|A') =
P(B'|A') = 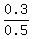 = =  ---------------------------
Edwin
---------------------------
Edwin
|
|
|