Question 515085: Asking again because email was entered wrong
Find the probability of the given value of x
mean = 28 standard deviation= 6.5 and x is equal to or less than 20
We are using the standard distribution z chart and I know it is plus or minus .5
However, I do not get the right answers
We are using z=x-u/o formula
Answer by drcole(72)   (Show Source):
You can put this solution on YOUR website! You have a random variable x that is normally distributed, with mean  and standard deviation  (these lowercase Greek letters are pronounced "mu" and "sigma" respectively. You need to figure out the probability that x is less than or equal to 20. You have the standard normal distribution table. How do we put this all together?
The idea here is we can change this problem on a non-standard normal distribution to one on the standard normal distribution by computing the z-score of 20. The z-score of 20 is simply the number of standard deviations 20 is above or below the mean. The formula you have tells you the z-score:
z-score =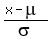 
Let's apply this formula:
z-score of 20 = 
This makes sense: 20 is more than one, but less than two standard deviations below the mean of 28, and a z-score of -1.23 is consistent with this observation.
It turns out that, if x is normally distributed, then the probability that x <= 20 is exactly the same as the probability that z, a random variable on the standard normal distribution, is less than or equal to the z-score of 20, or -1.23:
You can now use your table to find the probability that z <= -1.23. If your table gives probabilities for positive and negative z-scores, just look up -1.23 and read off the number. You should get:
or something very close to it (depending on how the values were rounded). If your table only gives probabilities for positive z-scores, then you can still get the right answer by observing that the standard normal distribution is symmetric: its bell curve shape is exactly the same on both sides of the mean. That means that the probability that z <= -1.23 is exactly the same as the probability that z >= 1.23, its mirror image. Since the probabilities that z <= 1.23 and z >= 1.23 should add to 1, we get that:
 (solving for P(z >= 1.23))
 (remembering that  )
So we look up the probability that z <= 1.23 in our table:
and then subtract the value we got from the table from 1 to get our answer:
which is exactly what we got before. Since the probability that x <= 20 is equal to the probability that z <= -1.23, this is our answer.
|
|
|
