Question 513966: a camera company surveyed 1000 people at random and asked how long film remianed in camera. 58% said less than one month, 20% said 1 to 3 months, and 22% said over 3 months. If a sample of 8 people who owned cameras is randomly selected, what is probability that 5 people have film that remianed in camera less than 1 month, 1 had film that remiained in camera 1 to 3 months, and 2 people had film that remianed in camera over 3 months?
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! The question gives three probabilities:
p = 0.58 = probability that film remained in camera less than one month
q = 0.20 = probability that film remained in camera one to three months
r = 0.22 = probability that film remained in camera over three months
Notice that p + q + r = 1. Because these are the only possible outcomes, we can find the probability above using a formula similar to that for binomial distributions. In general, if we take a sample of N people, and we want to split them into three groups, one of size k, one of size m, and one of size n, the number of ways we can do this is:
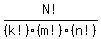
This is just an extension of the formula for the number of combinations. In this case, n = 8, k = 5, m = 1, and n = 2, so there are
 ways ways
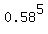
to arrange eight people in a group of five, a group of one, and a group of two. Now that we know how many ways to make this grouping, we need to know how likely such a grouping is. The probability that someone is in the first group is p = 0.58. Since the sample is randomly chosen, we can assume that the probabilities of two (or five) people being in this group are independent, so we can multiply the probabilities. So the probability of five people being in the first group is
Likewise, the probability of being in the second group is q = 0.20. The probability of being in the third group is r = 0.22, so the probability of two people in the third group is
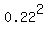
Finally, we multiply all of these probabilities together with the number of ways to arrange our group to get the final answer:

|
|
|