Question 478952: Nine tickets, numbered from 1 to 9, are in a box. If 2 tickets are drawn at random, determine the probability p that both are odd.
Here is how I did it:
P (2 tickets = odd, 9 tickets)
5 odd
9 tickets
P (2 tickets = odd, 9 tickets) = desired outcome/total outcome = (5/9) times (5/9) = (5/9)^2 = 25/81 = 0.3086 = 0.31
However, this is NOT the correct answer. My textbook says this:
5C2/9C2 = 5/18 = 0.28
Please note I would have solved this problem the textbook's way; yet, in a similar problem, I solved it the textbook's way and the book solved it the way I did in this problem. So, I corrected myself to proceed through the calculations as stated in my book. Now, the book switched on me. I don't know what is A DIFFERENCE between the two versions of the calculation. Percentages are slightly off, and I assume that my answer must be wrong since a slight difference in math means a huge gap.
If you do not mind, here is the similar problem I am referring to above: Three cards are drawn from a pack of 52 cards, each card being replaced before the next one is drawn. Compute the probability p that all are spades.
Here is how I did it: 13C3/52C3 = 0.0129 = 1.29 %
Here is how the textbook did it: (13/52)times(13/52)times(13/52) = (13/52)^3 = 0.0156 = 1.56%.
As you notice, the percentages are again just slightly off but still two different values. Please let me what am I missing? What is it that I solve the problem through combinations vs. (desired outcome/total outcome)^(number of drawings)?
Thank you very much for your time and advice. I really appreciate it. Have a beautiful and safe evening.
Respectfully,
Ivanka
Found 2 solutions by Earlsdon, Theo:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the ticket problem assumes no replacement.
the probability of drawing the first odd ticket is 5/9.
once you draw that ticket, without replacement, then then there are 4 odd tickets left out of a total of 8, so the probability of getting an odd ticket on the second draw is 4/8.
5/9 * 4/8 = 20/72 = 5/18
5C2/9C2 = 10/36 = 5/18
they're the same.
with your card problem, there is no replacement.
using combinations, the answer you show is:
13C3/52C3 = 286/22100 = .012941176
using probabilities, the answer would be 13/52 * 13/52 * 13/52 = .015625
the answer are not the same because replacement was assumed using the probabilties while no replacement was assumed when using the combination formulas.
that's the difference between each way.
the two different methods are comparable if you do not replace after every draw.
they are not comparable if you replace after every draw.
if you assumed no replacement in the card problem, then the probability would have been calculated as 13/52 * 12/51 * 11/50 = .012941176
the two methods are comparable in the card problem when you assume no replacement.
-----
if you look at 13C3 / 52C3 and work out the math, this is what you get:


13C3 / 52C3 becomes equal to:
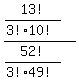
this is equivalent to:
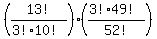
this can be rewritten as:
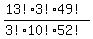
going a little further, this can be rewritten as:
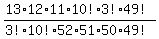
there's a 3! in the numerator and the denominator that cancels out.
there's a 10! in the numerator and the denominator that cancels out.
there's a 49! in the numerator and the denominator that cancels out.
your are left with:
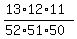
if you do the problem the alternate way using the probabilities for each event, then you get the same equation without replacement.
it is:
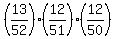 which can be rewritten as: which can be rewritten as:
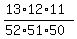
bottom line:
the two methods are comparable if you assume no replacement.
they are not comparable if you assume replacement.
|
|
|