SOLUTION: I have worked this one out but I am not sure if the answer is correct. I only get one shot so any assistance helps. A fair coin is flipped 20 times and the sequence of heads an

P(at least two heads) = 1-P(0 heads)-P(exactly 1 head)
 
P(0 heads).
The probability of 0 heads is the probability of all tails,
or ()20 =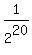 
 
P(exactly 1 head)
 
There are 10 sequences which would give this,
for the one head could come 1st, 2nd, 3rd,...
or tenth.
 
HTTTTTTTTT
THTTTTTTTT
TTHTTTTTTT
TTTHTTTTTT
TTTTHTTTTT
TTTTTHTTTT
TTTTTTHTTT
TTTTTTTHTT
TTTTTTTTHT
TTTTTTTTTH
 
The probability for each of these ten is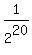 
So
 
P(exactly 1 head) =  
 
P(at least two heads) = 1-P(0 heads)-P(exactly 1 head)
P(at least two heads) = 
 
My numerator is 1048565, yours is 1048555
 
------------------------------------------------------------

Refer to the given graph. Assume one can move only down or to the right.
If a route starts at A and ends at C, what is the probability that the
route passes through B? Answer in fraction reduced to the lowest terms.
 
 A
[ ] [ ] [ ]B[ ] [ ]
[ ] [ ] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ]C
 
 
Let's number the vertical columns 1-5
and the horizontal rows 1-5:
Notice that each path from A to C can be
identified by 4 numbers, the column on which
the path drop to the next row. For instance this path
 
        col col col col col 
         1   2   3   4   5
         |   |   |   |   |
         A
row 1   [x] [x] [ ]B[ ] [ ]
row 2   [ ] [x] [ ] [ ] [ ]
row 3   [ ] [x] [x] [x] [ ]
row 4   [ ] [ ] [ ] [x] [ ]
row 5   [ ] [ ] [ ] [x] [x]C
 

This path which does not go through B could be
identified as (2,2,4,4) because 
 
The 1st drop from row 1 to row 2 is at column 2
The 2nd drop from row 2 to row 3 is at column 2
The 3rd drop from row 3 to row 4 is at column 4
The 4th drop from row 4 to row 5 is at column 4
 
For another example instance this path
 
        col col col col col 
         1   2   3   4   5
         |   |   |   |   |
         A
row 1   [x] [x] [x]B[x] [ ]
row 2   [ ] [ ] [ ] [x] [ ]
row 3   [ ] [ ] [ ] [x] [ ]
row 4   [ ] [ ] [ ] [x] [x]
row 5   [ ] [ ] [ ] [ ] [x]C
 

This path which does go through B could be
identified as (4,4,4,5) because 
 
The 1st drop from row 1 to row 2 is at column 4
The 2nd drop from row 2 to row 3 is at column 4
The 3rd drop from row 3 to row 4 is at column 4
The 4th drop from row 4 to row 5 is at column 5
 
So we need to know how many of these exist.
They all consist of 4 integers from 1 to 5, inclusive,
arranged in numerical order from smallest to largest.

There are 4 types of these.
1.  Those that contain exactly 1 number, (x,x,x,x)
    There are C(5,1) = 5 of these,
    (1,1,1,1), (2,2,2,2), (3,3,3,3), (4,4,4,4), (5,5,5,5)  

2.  Those that contain exactly 2 numbers are of these 3 forms
    (x,x,x,y), (x,x,y,y), (x,y,y,y) where x < y.
    So that's 3*C(5,2) or 3*10 = 30 more 
    
3.  Those that contain exactly 3 numbers are of these 3 forms 
    (x,x,y,z), (x,y,y,z), {x,y,z,z) where  x < y < z.
    So that 3*C(5,3) = 3*10 = 30 more    

4.  Those that contain exactly 4 numbers (x,y,z,w) where
    x < y < z < w are C(5,4) = 5

So that's a total of 5+30+30+5 = 70

That's the denominator of the desired probability.

Of those 70 ways to get from A to C only those whose first
drop is at either 4 or 5 will go through B.  They are

(4,4,4,4), (4,4,4,5), (4,4,5,5), (4,5,5,5) and (5,5,5,5)
  
So the desired probability is 5/70 which reduces to 1/14

Edwin