Question 441203: 3.18 Suppose A and B are events with 0 < P(A) < 1 and 0 < P(B) < 1.
a. If A and B are disjoint, can they be independent?
b. If A and B are independent, can they be disjoint?
c. If A ⊂ B, can A and B be independent?
d. If A and B are independent, can A and A ∪ B be independent
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. A, B disjoint means P(A and B) = 0. Since P(A), P(B) > 0, 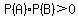 , hence , hence 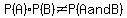 , and so are not independent. , and so are not independent.
b. A, B independent means 
==> 
Unless P(A)*P(B)= 0, A and B can never be disjoint. But from the given, P(A)*P(B) > 0, hence A, B are never disjoint.
c. If A ⊂ B, then P(A and B) = P(A). If we assume independence, then
P(A) = P(A)*P(B), which means
P(B) = 1, a contradiction of the hypothesis that 0 < P(B) < 1. Hence A, B are not independent.
d. P(A and (A ∪ B)) = P(A), since A ⊂ A U B. Hence the argument is reduced to one like in part (c) above, the result being the same.
|
|
|