SOLUTION: A clothing store owner knows from previous records that any person who comes into her store has a 60 percent chance of making a purchase. She notes that there are 13 people in her

Algebra ->  Probability-and-statistics -> SOLUTION: A clothing store owner knows from previous records that any person who comes into her store has a 60 percent chance of making a purchase. She notes that there are 13 people in her      Log On


   

Question 387941: A clothing store owner knows from previous records that any person who comes into her store has a 60 percent chance of making a purchase. She notes that there are 13 people in her store at the current time. What is the probability that:
a. exactly 5 people will make a purchase?
b. less than 8 people make a purchase?
c. More than 10 people make a purchase?
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi,         

Note: The probability of x successes in n trials is: P = nCx* p%5Ex%2Aq%5E%28n-x%29

 where p and q are the probabilities of success and failure respectively. 

In this case p =.6 and  q = .4

nCx = 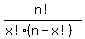n%21%2F%28x%21%28n-x%21%29%29

for example:

P(exactly 5 people will make a purchase)= 1287(.6)^5(.4)^8 = .06559



P(less than 8 people make a purchase)  

1- P(8) - P(9) - P(10) - P(11)- P(12) - P(13) = .4256  (Stat Trek)



P(More than 10 people make a purchase) = P(11) +  P(12) + P(13)  

 P(11) +  P(12) + P(13) = .04528 + .01132 + .00131 = .0579