Question 278589: Ten pair of shoes are kept in a rack.If four shoes are selected at random what is the probability that there is atleast one pair among them
Found 5 solutions by stanbon, edjones, Grinnell, geekyengineer, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ten pair of shoes are kept in a rack.If four shoes are selected at random what is the probability that there is at least one pair among them
------------------
There are ten shoes that do not contain a pair.
---
P(at least one pair) = 1-P(no pair)
---
P(no pair in the shoes selected) = 10C4/20C4 = 210/4845
--------
Therefore P(at least one pair) = 1 - 210/4845 = 4635/4845 = 0.9567
======================================================================
Cheers,
Stan H.
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! After the 1st shoe removed 1/19 that its brother will be chosen. after a second removed then 2/18 chance and after 3rd chosen 3/17.
1/19 + 2/18 + 3/17 = .34
I am not 100% sure that this correct.
Let me know.
.
Ed
Answer by Grinnell(63)   (Show Source): (Show Source):
You can put this solution on YOUR website! Another deceptive problem!!!!!
Out of the 20 shoes there are ten pairs.
Since we are trying to choose pairs,
4 selections of shoes are the same as 2
selections (attempts) at 1 pair.
Two (pair selections) picks out a 1/10 chance
at a pair would be 20%!
If anyone comes up with anything different, let me know.
Have not cracked prob. books in a while.
Thanks!
Answer by geekyengineer(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! If four shoes selected at random the probability of at least one pair will be given by = 1 - p(no pair will be selected)
p(no pair will be selected) = (10C4 * 2^4)/(20C4) = 0.6934
Hence, required probabilty = 1 - 0.6934 = 0.3065
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Ten pair of shoes are kept in a rack.If four shoes are selected at random what is the probability that there is atleast one pair among them
~~~~~~~~~~~~~~~~~~~
Solution
Let's assume that the shoes are numbered by integer numbers from 1 to 20 in a way that
the first pair is (1,2),
the second pair is (3,4),
the third pair is (4,5),
. . . and so on . . .
the tenth pair is (19,20).
The full space of samples is the space of quadruples of different shoes taken from 20 at a time.
(it is the same as the set of all subsets consisting of 4 elements of the original set of 20 shoes).
So, the total number of elements of this sample space is 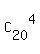 = = 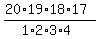 = 4845.
Very good.
Now I want to figure out, in how many ways I can choose 4 shoes in a way that there is NO pair/pairs among them.
Obviously, for it, I should choose these 4 shoes from DIFFERENT PAIRS.
In this way, I get the number of such quadruples as = 4845.
Very good.
Now I want to figure out, in how many ways I can choose 4 shoes in a way that there is NO pair/pairs among them.
Obviously, for it, I should choose these 4 shoes from DIFFERENT PAIRS.
In this way, I get the number of such quadruples as  = = 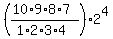 = 3360.
The factor = 3360.
The factor 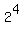 is due to the fact that there is the choice of one of two shoes inside each pair.
So, the probability under the question is is due to the fact that there is the choice of one of two shoes inside each pair.
So, the probability under the question is 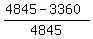 = =  = =  = 0.3065 = 30.65%. ANSWER = 0.3065 = 30.65%. ANSWER
Solved.
/\/\/\/\/\/\/\/\/\/
My solution produces the same answer as the other tutor provides;
but I hope it gives more clear explanation on how the solution was obtained.
With it, my congratulations to tutor @geekyengineer, who found a brilliant solution !
|
|
|