Question 245774: A given locality has the telephone prefix of 237.
a. How many seven-digit phone numbers are possible with this prefix?
b. How many of these possibilities have four ending numbers that are all equal?
c. What is the probability of having one of the numbers in part (b)?
d. What is the probability that the last four digits are consecutive (i.e.,1234)?
Thank you,
Marney
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. Assuming that no numbers are excluded (like numbers that start with 555- which are not assigned), then there are 10 possible choices for each of the digits. So there are 10*10*10*10*10*10*10 or 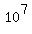 possibilities. possibilities.
b. We can pick any numbers for the first three numbers. We can even pick any number for the fourth digit. But once the fourth digit is chosen, the remaining three must be the same (i.e. there is only one choice for each of the last 3 digits) because we want the last 4 digits to be the same. So the number of possible numbers with the last 4 digits equal will be 10*10*10*10*1*1*1 or 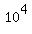 . .
c. The probability of a number with the last four digits equal is
the number of phone numbers with the last 4 digits equal
--------------------------------------------------------
the total number of possible phone numbers
We figured out these numbers in parts (a) and (b):

d. The probability of a number with the last four digits conseuctive is
the number of phone numbers with the last 4 digits consecutive
--------------------------------------------------------------
the total number of possible phone numbers
We know the denominator from part (a). We need to figure out the numerator.
Again the first three digits can be any numbers. The fourth digit must be less than 7. This is so because if the fourth digit was 7, 8 or 9 then it would be impossible for the next three to be conseuctive: xxx-789?, xxx-89?? xxx-9???. So there are only 7 possible 4th digits (0, 1, 2, 3, 4, 5, or 6). After the 4th digit is chosen there is only one choice for the next digit because there is only one "next" number. For the same reason there will be only one choice for the 6th and 7th digits. So the number of phone numbers with the last 4 digits consecutive is 10*10*10*7*1*1*1 = 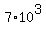 . This makes the probability . This makes the probability

|
|
|