You can
put this solution on YOUR website! two dice are thrown, the probability that the number on the red exceeds the number showing on the green by exactly two is
a) 1/18 b) 1/4 c) 1/9 d)1/36 e) 1/24
-----------------------------------------------
# of possible outcomes with two dice: 36
patterns with red exceeding green by 2:1;4,2;5,3;6,
=========================================
Probability is 4/36 = 1/9
====================================
Cheers,
Stan H.
-----------------
PS: Respond to stanbon@comcast.net as the algebra.com
feedback program is down.
---------------------------
You can
put this solution on YOUR website!Two dice are thrown, the probability that the number on the red exceeds the number showing on the green by exactly two is
a) 1/18 b) 1/4 c) 1/9 d)1/36 e) 1/24
Here are all the possible rolls with a
red die and a green die:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 possible rolls. Now I
will underline just those in which
the number on the red exceeds the
number showing on the green by exactly
two:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 possible rolls. So
there are 4 possible rolls out of
the 36 which have that property.
Therefore the probability is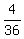 
which reduces to 
Edwin
(