A deck of 40 cards contains 10 green cards, 29 blue cards, and 1 red card.
The first card you draw is the red card.
So what you have now is a deck of 39 cards containing 10
green cards and 29 blue cards.
You draw 6 other cards without replacement.
What is the probability that at least one of those 6 cards is green?
We use the complement event, and then subtract its probability from 1.
The complement event is to draw 6 non-green cards in a row.
There are 29 non-green cards, so the probability of drawing
a non-green card the first time is 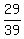 .
Now there are 28 non-green cards, so the probability of drawing
a non-green card the second time is
.
Now there are 28 non-green cards, so the probability of drawing
a non-green card the second time is 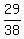 .
Now there are 27 non-green cards, so the probability of drawing
a non-green card the third time is
.
Now there are 27 non-green cards, so the probability of drawing
a non-green card the third time is 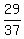 .
Now there are 26 non-green cards, so the probability of drawing
a non-green card the fourth time is
.
Now there are 26 non-green cards, so the probability of drawing
a non-green card the fourth time is 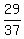 .
Now there are 25 non-green cards, so the probability of drawing
a non-green card the fifth time is
.
Now there are 25 non-green cards, so the probability of drawing
a non-green card the fifth time is 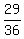 .
Now there are 24 non-green cards, so the probability of drawing
a non-green card the sixth time is
.
Now there are 24 non-green cards, so the probability of drawing
a non-green card the sixth time is 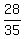 .
So the probability of drawing a non-green card each of those
six times is the product of those probabilities
.
So the probability of drawing a non-green card each of those
six times is the product of those probabilities
 Then
Then  Edwin
Edwin