Question 1210439: Trey wakes up late on average 4 days out of every 5. If Trey wakes up late, the probability that he is late for school is 90%. If Trey doesn't wake up late the probability that he is late for school is 25%. Create a tree diagram by entering the percentages and then calculate the percent chance that Trey gets to school on time.
Enter your answers as a decimal or fraction between 0 and 1.
Answer by ikleyn(52967)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Trey wakes up late on average 4 days out of every 5. If Trey wakes up late, the probability that he is late
for school is 90%.
If Trey doesn't wake up late the probability that he is late for school is 25%.
Create a tree diagram by entering the percentages and then calculate the percent chance
that Trey gets to school on time.
Enter your answers as a decimal or fraction between 0 and 1.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will not create a tree diagram. Instead, I will use my logic skills.
First, we have 4 days out every 5 days, when Trey wakes up late.
In these 4 days, the probability that Trey gets school on time is (1-0.9) = 0.1.
So, these 4 days contribute 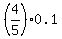 = 0.8*0.1 = 0.08 to the sough probability.
Next, we have 1 day out every 5 days when Trey doesn't wake up late.
In this day, the probability he gets the school on time is (1-0.25) = 0.75.
So, this remarkable day contributes = 0.8*0.1 = 0.08 to the sough probability.
Next, we have 1 day out every 5 days when Trey doesn't wake up late.
In this day, the probability he gets the school on time is (1-0.25) = 0.75.
So, this remarkable day contributes 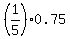 = 0.2*0.75 = 0.15 to the sough probability.
Now we add two partial probabilities 0.08 and 0.15, and we get the answer
P = 0.08 + 0.15 = 0.23.
At this point, we complete the solution. = 0.2*0.75 = 0.15 to the sough probability.
Now we add two partial probabilities 0.08 and 0.15, and we get the answer
P = 0.08 + 0.15 = 0.23.
At this point, we complete the solution.
Solved.
|
|
|