Question 1210432: A CBS News poll conducted June 10 and 11, 2006, among a nationwide random sample of 651 adults, asked those adults about their party affiliation (Democrat, Republican or none) and their opinion of how the US economy was changing (getting better," "getting worse" or "about the same"). The results are shown in the table below.
better same worse
Republican 38 104 44
Democrat 12 87 137
none 21 90 118
Express your answers as a decimal and round to the nearest 0.001 (in other words, type 0.123, not 12.3% or 0.123456).
If we randomly select one of the adults who participated in this study, compute:
P (Democrat) =
P(same) =
P(Democrat and same) =
Answer by ikleyn(52968)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A CBS News poll conducted June 10 and 11, 2006, among a nationwide random sample of 651 adults, asked those adults
about their party affiliation (Democrat, Republican or none) and their opinion of how the US economy was changing
(getting better," "getting worse" or "about the same"). The results are shown in the table below.
better same worse
Republican 38 104 44
Democrat 12 87 137
none 21 90 118
Express your answers as a decimal and round to the nearest 0.001 (in other words, type 0.123, not 12.3% or 0.123456).
If we randomly select one of the adults who participated in this study, compute:
(a) P (Democrat) =
(b) P(same) =
(c) P(Democrat and same) =
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
S O L U T I O N
(a) To calculate the probability for (a), we should add the numbers of democrats in all three cells of the second line
n(democrats) = 12 + 87 + 137 = 236.
To answer (a), we should relate this number of all surveyed democrats, 236, to the total number 651 in the sample
P(Democrat) =  = = 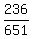 = 0.363.
I rounded it with 3 places after the decimal dot, as you requested.
(b) To calculate the probability for (b), we should add the numbers in column 2 (under the name "same")
n(same) = 104 + 87 + 90 = 281.
To answer (b), we should relate this number of all answered "same", 281, to the total number 651 in the sample
P(Democrat) = = 0.363.
I rounded it with 3 places after the decimal dot, as you requested.
(b) To calculate the probability for (b), we should add the numbers in column 2 (under the name "same")
n(same) = 104 + 87 + 90 = 281.
To answer (b), we should relate this number of all answered "same", 281, to the total number 651 in the sample
P(Democrat) = 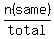 = = 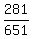 = 0.432.
I rounded it with 3 places after the decimal dot, as you requested.
(c) To calculate the probability for (c), we should take the numbers in the intersection of line "Democrat"
with column "same"
n(Democrat and same) = 90.
To answer (c), we should relate this number, 87, to the total number 651 in the sample
P(Democrat and same) = = = 0.432.
I rounded it with 3 places after the decimal dot, as you requested.
(c) To calculate the probability for (c), we should take the numbers in the intersection of line "Democrat"
with column "same"
n(Democrat and same) = 90.
To answer (c), we should relate this number, 87, to the total number 651 in the sample
P(Democrat and same) = = 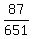 = 0.134.
I rounded it with 3 places after the decimal dot, as you requested. = 0.134.
I rounded it with 3 places after the decimal dot, as you requested.
At this point, the problem is solved completely: all questions are answered with all necessary explanations.
Happy learning !
--------------------------------------
I am very impressed on how accurately did you presented your problem this time.
If you will be so accurate in your job, people will see it, and a great future awaits you !
Come again to this forum soon to learn something new !
|
|
|