SOLUTION: A grocer's bin contains 7 ripe tomatoes and 9 unripened tomatoes. Three tomatoes are selected at random (Tomatoes are not replaced). Show the probability distribution for the nu

Algebra ->  Probability-and-statistics -> SOLUTION: A grocer's bin contains 7 ripe tomatoes and 9 unripened tomatoes. Three tomatoes are selected at random (Tomatoes are not replaced). Show the probability distribution for the nu      Log On


   

Question 1210330: A grocer's bin contains 7 ripe tomatoes and 9 unripened tomatoes. Three tomatoes are selected at random (Tomatoes are not replaced). Show the probability distribution for the number of ripe tomatoes.



Found 3 solutions by mccravyedwin, ikleyn, math_tutor2020:
Answer by mccravyedwin(407) About Me  (Show Source):
You can put this solution on YOUR website!
>>>A grocer's bin contains 7 ripe tomatoes and 9 unripened tomatoes.<<<  

So altogether there are 7+9=16 tomatoes in the grocer's bin.

>>>Three tomatoes are selected at random  (Tomatoes are not replaced).<<<

He chooses one of these 4 groups of 3 tomatoes: 

0 ripe tomatoes and 3 unripened tomatoes.
1 ripe tomato and 2 unripened tomatoes.
2 ripe tomatoes and 1 unripened tomato.
3 ripe tomatoes and 0 unripened tomatoes.

>>>Show the probability distribution for the number of ripe tomatoes.<<<

P%28matrix%281%2C3%2C0%2Cripe%2Ctomatoes%29%29%22%22=%22%22%28C%287%2C0%29%2AC%289%2C3%29%29%2FC%2816%2C3%29%22%22=%22%22%281%2A84%29%2F560%22%22=%22%2284%2F560%22%22=%22%223%2F20%22%22=%22%220.15

P%28matrix%281%2C3%2C1%2Cripe%2Ctomato%29%29%22%22=%22%22%28C%287%2C1%29%2AC%289%2C2%29%29%2FC%2816%2C3%29%22%22=%22%22%287%2A36%29%2F560%22%22=%22%22252%2F560%22%22=%22%229%2F20%22%22=%22%220.45

P%28matrix%281%2C3%2C2%2Cripe%2Ctomatoes%29%29%22%22=%22%22%28C%287%2C2%29%2AC%289%2C1%29%29%2FC%2816%2C3%29%22%22=%22%22%2821%2A9%29%2F560%22%22=%22%22189%2F560%22%22=%22%2227%2F80%22%22=%22%220.3375

P%28matrix%281%2C3%2C3%2Cripe%2Ctomatoes%29%29%22%22=%22%22%28C%287%2C3%29%2AC%289%2C0%29%29%2FC%2816%2C3%29%22%22=%22%22%2835%2A1%29%2F560%22%22=%22%2235%2F560%22%22=%22%221%2F16%22%22=%22%220.0625

Observe that the sum of those 4 probabilities is

0.15 + 0.45 + 0.3375 + 0.0625 = 1.  That's because it is certain that one of
those 4 events must occur.

Edwin

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
A grocer's bin contains 7 ripe tomatoes and 9 unripened tomatoes.
Three tomatoes are selected at random (Tomatoes are not replaced).
Show the probability distribution for the number of ripe tomatoes.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Let x be the number of ripe tomatoes in our random sample of 3 tomatoes.

They want you find and present the numbers  P(x=0),  P(x=1),  P(x=2)  and  P(x=3).



(0)  x=0  means that in our sample all 3 tomatoes are unripped; there is no ripped tomatoes.

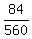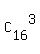     So, P(x=0) = C%5B9%5D%5E3%2FC%5B16%5D%5E3 = 84%2F560 = 3%2F20.

     Here  C%5B16%5D%5E3 = 560 in the denominator is the total number of triples of 16 = 7+9 tomatoes.

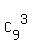           C%5B9%5D%5E3 = 84 in the numerator is the number of triples of 9 unripped tomatoes.




(1)  x = 1  means that in our sample 1 tomato is ripped; two other tomatoes are unripped.

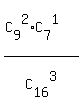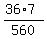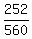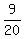     So, P(x=1) = %28C%5B9%5D%5E2%2AC%5B7%5D%5E1%29%2FC%5B16%5D%5E3 = %2836%2A7%29%2F560 = 252%2F560 = 9%2F20.

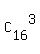     Again, here  C%5B16%5D%5E3 = 560 in the denominator is the total number of triples of 16 = 7+9 tomatoes.

           C%5B9%5D%5E2%2AC%5B7%5D%5E1 = 36*7 = 252 in the numerator is the number of triples, 
                                      consisting of 2 unripped tomatoes and 1 ripped tomato.




(2)  x = 2  means that in our sample 2 tomatoes are ripped; one tomato is unripped.

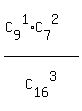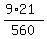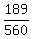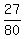     So, P(x=2) = %28C%5B9%5D%5E1%2AC%5B7%5D%5E2%29%2FC%5B16%5D%5E3 = %289%2A21%29%2F560 = 189%2F560 = 27%2F80.

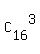     Again, here  C%5B16%5D%5E3 = 560 in the denominator is the total number of triples of 16 = 7+9 tomatoes.

           C%5B9%5D%5E1%2AC%5B7%5D%5E2 = 9*21 = 189 in the numerator is the number of triples, 
                                      consisting of 1 unripped tomato and 2 ripped tomatoes.



(3)  x = 3  means that in our sample 3 tomatoes are ripped; no unripped tomatoes.

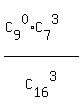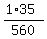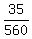     So, P(x=3) = %28C%5B9%5D%5E0%2AC%5B7%5D%5E3%29%2FC%5B16%5D%5E3 = %281%2A35%29%2F560 = 35%2F560 = 1%2F16   after reducing.

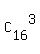     Again, here  C%5B16%5D%5E3 = 560 in the denominator is the total number of triples of 16 = 7+9 tomatoes.

           C%5B9%5D%5E0%2AC%5B7%5D%5E3 = 1*35 = 35 in the denominator is the number of triples, 
                                      consisting of 0 unripped tomatoes and 3 ripped tomatoes.


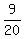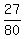Thus  P(0) = 3%2F20;  P(1) = 9%2F20;  P(2) = 27%2F80;  P(3) = 1%2F16 = 5%2F80.


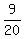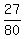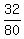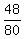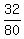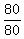The sum  P(0) + P(1) + P(2) + P(3) = 3%2F20 + 9%2F20 + 27%2F80 + 5%2F80 = 12%2F20 + 32%2F80 = 48%2F80 + 32%2F80 = 80%2F80 = 1.

Solved.




Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

The other tutors are using the combination formula.

I'll show an example calculation.
C(n,r) = (n!)/(r!(n-r)!)
C(7,3) = (7!)/(3!*(7-3)!)
C(7,3) = (7!)/(3!*4!)
C(7,3) = (7*6*5*4!)/(3!*4!)
C(7,3) = (7*6*5)/(3!)
C(7,3) = (7*6*5)/(3*2*1)
C(7,3) = 210/6
C(7,3) = 35
This indicates there are 35 ways to select 3 ripe tomatoes from a pool of 7 ripe tomatoes, where order doesn't matter. This assumes that we can distinguish the tomatoes apart.
C(7,3) = 35 is equivalent to saying 7C3 = 35.

Note that 35 is found in Pascal's Triangle. Locate the row that starts with "1,7,..."
In that row, move 3 spots to the right and you should land on 35. Specifically you should land on the first copy of 35.
n = 7 tells us which row to look at, while r = 3 tells us how far to move to the right.

In GeoGebra, you would type ncr(7,3) to compute the combination value.
Many other online calculators can be used as well. Or you can use a spreadsheet.
If you want to use Desmos, then you would input nCr(7,3) where the C must be uppercase and everything else lowercase.