Question 1207704: Alex chooses a number at random from the set $\{1, 2, 3, \dots, 5\}.$ Winnie also chooses a number at random from the same set. (They can choose the same number.) What is the probability that the product of their numbers is at least 3?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Alex chooses a number at random from the set {1, 2, 3, . . . , 5}.
Winnie also chooses a number at random from the same set.
(They can choose the same number.)
What is the probability that the product of their numbers is at least 3?
~~~~~~~~~~~~~~~~~~~~
In all, there are TOTAL = 5*5 = 25 different pairs of numbers to choose from the table.
Of these 25 pairs, the FAVORABLE pairs are all except (1,1), (1,2), (2,1).
So, the probability that the product of their numbers is at least 3
P =  = = 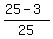 = = 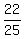 = 0.88 = 88%. ANSWER = 0.88 = 88%. ANSWER
Solved.
/\/\/\/\/\/\/\/
Hello, in your post, the ellipses are used to replace only one number, 4.
Such use of ellipses makes me smile.
(Because normally people never write this way).
I think that many other will also smile reading it . . .
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are 5x5=25 ways they can choose a number.
The only way they can fail to have a product of at least 3 is for:
1. both to choose a 1
2. Alex to choose a 1 and Winnie to choose a 2.
3. Alex to choose a 2 and Winnie to choose a 1.
Any other choices will be successful.
The probability of a failure is 3/25. Therefore,
the probability of a success is 22/25 = 88%
Edwin
|
|
|