Question 1207461: Please resolve this question. You have two 10 cents coins, two $1 coins, one fifty cents coin and a $2 coin. one coin is randomly chosen and is not replaced. two more coins are then randomly chosen, What is the total number of possible outcomes for this chance experiment.
Found 4 solutions by Edwin McCravy, mccravyedwin, ikleyn, AnlytcPhil:
Answer by Edwin McCravy(20054)   (Show Source):
Answer by mccravyedwin(406)  (Show Source):
You can put this solution on YOUR website! I made a mistake on my first solution. Here is the correct version:
The values of the coins are irrelevant. Also, the probabilities of
selecting coins is also irrelevant. [In future problems like this
they will be relevant].
But all that matters is that you started with 6 coins, two pairs
and two singles, where each member of each pair is indistinguishable
from the other member of that pair. Say, the 6 coins are AABBCD.
Case 1. You choose one of the A's not to replace. You have left ABBCD.
You can then choose AB,AC,AD,BB,BC,BD,CD
There are 7 outcomes.
Case 2. You choose one of the B's not to replaced. Same as case 1.
There are 7 outcomes.
Case 3. You choose the C not to replace. You have left AABBD.
You can then choose AA,AB,AD,BB,BD
There are 5 outcomes.
Case 4. You choose the D not to replace. Same as case 3.
There are 5 outcomes.
Total = 7+7+5+5=22 possible outcomes.
Edwin
Answer by ikleyn(52777)  (Show Source):
You can put this solution on YOUR website! .
Please resolve this question. You have two 10 cents coins, two $1 coins, one fifty cents coin and a $2 coin.
one coin is randomly chosen and is not replaced. two more coins are then randomly chosen,
What is the total number of possible outcomes for this chance experiment.
~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by Edwin is incorrect.
It is incorrect, since Edwin counts many identical outcomes as different outcomes.
I apply totally different logic and obtain totally different solution and answer.
The problem's question is the same (= is equivalent) as to ask
having two 10-cent coins, two 1-dollar coins, one 50-cent coin and one 2-dollar coin,
in how many different ways can you choose a triple of coins (without looking on the order).
Had all 6 coins be different, we would choose 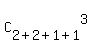 =  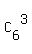=  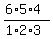= 5*4 = 20
different triples.
But some triples are indistinguishable, because they have indistinguishable coins;
therefore, we should count indistinguishable triples only ONCE, NOT twice.
So, you have the set AABBCD to start choosing triples from it.
All unique distinct triples are
ABC (no repetition)
ABD (no repetition)
ACD (no repetition)
BCD (no repetition)
AAB (with repeating A)
AAC (with repeating A)
AAD (with repeating A)
ABB (with repeating B)
BBC (with repeating B)
BBD (with repeating B)
Thus these 10 outcomes are all possible different outcomes in this experiment. ANSWER
Solved.
Hope Edwin will agree with this solution,
and we will celebrate the triumph of reason together.
Answer by AnlytcPhil(1806)  (Show Source):
You can put this solution on YOUR website!
It depends on what you mean by "outcome"
I took "outcome" to mean "situation".
Ikleyn took "outcome to mean "coins drawn"
For instance, I considered A|BB and B|AB as two different outcomes.
She took them as the same outcome.
I guess she's right. I possibly misinterpreted what "outcome" meant.
Edwin
|
|
|
