Question 1206991: Problem 6.(3 points)
A breathalyser test is used by police in an area to determine
whether a driver has an excess of alcohol in their blood. The de-
vice is not totally reliable: 7 % of drivers who have not consumed
an excess of alcohol give a reading from the breathalyser as being
above the legal limit, while 10 % of drivers who are above the le-
gal limit will give a reading below that level. Suppose that in fact
17 % of drivers are above the legal alcohol limit, and the police
stop a driver at random. Give answers to the following to four
decimal places.
Part a)
What is the probability that the driver is incorrectly classified as
being over the limit?
Part b)
What is the probability that the driver is correctly classified as be-
ing over the limit?
Part c)
Find the probability that the driver gives a breathalyser test read-
ing that is over the limit.
Part d)
Find the probability that the driver is under the legal limit, given
the breathalyser reading is also below the limit.
Answer by ikleyn(52754)   (Show Source):
You can put this solution on YOUR website! .
Problem 6.(3 points)
A breathalyser test is used by police in an area to determine whether a driver has an excess of alcohol in their blood.
The device is not totally reliable: 7 % of drivers who have not consumed an excess of alcohol give a reading from
the breathalyser as being above the legal limit, while 10 % of drivers who are above the legal limit will give a reading below that level.
Suppose that in fact 17 % of drivers are above the legal alcohol limit, and the police stop a driver at random.
Give answers to the following to four decimal places.
(a) What is the probability that the driver is incorrectly classified as being over the limit?
(b) What is the probability that the driver is correctly classified as being over the limit?
(c) Find the probability that the driver gives a breathalyser test reading that is over the limit.
(d) Find the probability that the driver is under the legal limit, given the breathalyser reading is also below the limit.
~~~~~~~~~~~~~~~~
(a) In (a), they want you determine the probability of two simultaneous events:
the driver is under the limit, but the reading incorrectly classified him
as being over the limit.
The ANSWER to (a) is (1-0.17)*0.07 = 0.0581.
(b) In (b), they want you determine the probability of two simultaneous events:
the driver is over the limit, and the reading correctly classified him
as being over the limit.
The ANSWER to (b) is 0.17*(1-0.1) = 0.153 = 15.3%.
(c) This probability is the sum of two probabilities of disjoint events:
- the driver is under the limit (1-0.17), but the reading is mistakenly over the limit
P = (1-0.17)*0.07;
- the driver is over the limit (0.17), and the reading is correctly over the limit
P = 0.17*0.9.
Therefore, the probability in (c) is P = (1-0.17)*0.07 + 0.17*0.9 = 0.2111. ANSWER to (c)
(d) In (d), the conditional probability is
P = 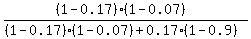 =  = 0.978451. ANSWER to (d)
In this formula, the numerator is the probability of the event that the driver is under the legal limit
and the reading is under the legal limit.
The denominator is the probability that the reading is below the legal limit.
Solved.
|
|
|
