Question 1206646: According to The World Bank, only 9% of the population of Uganda had access to electricity as of 2009. Suppose we randomly sample 145 people in Uganda. Let X = the number of people who have access to electricity.
(a) What is the probability distribution for X?
X ~ G(145)
X ~ B(145, 0.09)
X ~ P(0.09)
X ~ G(0.09)
X ~ B(0.09, 145)
(b) Using the formulas, calculate the mean and standard deviation of X. (Enter your mean to two decimal places and round your standard deviation to four decimal places.)
(c) Use your calculator to find the probability that 15 people in the sample have access to electricity. (Round your answer to four decimal places.)
(d) Find the probability that at most ten people in the sample have access to electricity. (Round your answer to four decimal places.)
(e) Find the probability that more than 25 people in the sample have access to electricity. (Round your answer to four decimal places.)
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
According to The World Bank, only 9% of the population of Uganda had access to electricity as of 2009.
Suppose we randomly sample 145 people in Uganda. Let X = the number of people who have access to electricity.
(a) What is the probability distribution for X?
X ~ G(145)
X ~ B(145, 0.09)
X ~ P(0.09)
X ~ G(0.09)
X ~ B(0.09, 145)
(b) Using the formulas, calculate the mean and standard deviation of X.
(Enter your mean to two decimal places and round your standard deviation to four decimal places.)
(c) Use your calculator to find the probability that 15 people in the sample have access to electricity.
(Round your answer to four decimal places.)
(d) Find the probability that at most ten people in the sample have access to electricity.
(Round your answer to four decimal places.)
(e) Find the probability that more than 25 people in the sample have access to electricity.
(Round your answer to four decimal places.)
~~~~~~~~~~~~~~~~~~~~~~~
(a) It is a binomial distribution with n= 145 trials and the probability of success p= 0.09
for each individual trial.
I do not understand the meaning of these hieroglyphs under (a), so you should determine it on your own.
(b) The mean for this binomial distribution is m = n*p = 0.09*145 = 13.05.
The standard deviation is SD = 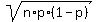 = =  = 3.446084735.
Questions (c), (d) and (e) assume that you will use normal distribution formulas for this binomial distribution
as an approximation. Statistically, it is possible because the number of trials n= 145 is great.
(c) Use your regular calculator TI-83/84 with standard function normcdf
(which stands for Cumulative Distribution Function).
For (c), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval (14.5,15.5). This interval "with plus/minus halves" is the continuous correction, when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( 14.5, 15.5, 13.05, 3.446084735).
Alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
To be honest, I always use it in my calculations, since it has simple and very convenient interface
and great visual output.
You can be restricted in using calculators, so use whichever is an appropriate for you.
In any case, the answer for (c) is P = 0.0984.
(d) For (d), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval ( = 3.446084735.
Questions (c), (d) and (e) assume that you will use normal distribution formulas for this binomial distribution
as an approximation. Statistically, it is possible because the number of trials n= 145 is great.
(c) Use your regular calculator TI-83/84 with standard function normcdf
(which stands for Cumulative Distribution Function).
For (c), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval (14.5,15.5). This interval "with plus/minus halves" is the continuous correction, when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( 14.5, 15.5, 13.05, 3.446084735).
Alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
To be honest, I always use it in my calculations, since it has simple and very convenient interface
and great visual output.
You can be restricted in using calculators, so use whichever is an appropriate for you.
In any case, the answer for (c) is P = 0.0984.
(d) For (d), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval ( , ,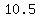 ). This interval is the continuous correction to "at most 10", when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( -9999, 10.5, 13.05, 3.446084735).
Again, alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
In any case, the answer for (d) is P = 0.2297.
(e) For (e), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval ( ). This interval is the continuous correction to "at most 10", when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( -9999, 10.5, 13.05, 3.446084735).
Again, alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
In any case, the answer for (d) is P = 0.2297.
(e) For (e), the probability is the area under the normal curve (with the mean and standard deviation determined in (a))
in the interval (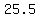 , , ). This interval is the continuous correction to "more than 25", when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( 25.5, 9999, 13.05, 3.446084735).
Again, alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
In any case, the answer for (e) is P = 0.0002.
It is a vanishing value; when the value of probability is vanishing, normal approximation works badly
(consider it as my warning to you). ). This interval is the continuous correction to "more than 25", when we use normal
distribution as an approximation to binomial. So, we write
z1 z2 mean SD <<<---=== formatting pattern
P = normcdf( 25.5, 9999, 13.05, 3.446084735).
Again, alternatively, you may use free of charge online calculator for normal distribution
https://onlinestatbook.com/2/calculators/normal_dist.html
In any case, the answer for (e) is P = 0.0002.
It is a vanishing value; when the value of probability is vanishing, normal approximation works badly
(consider it as my warning to you).
At this point, I complete my solution.
--------------
It is not a simple task to write so long text - - - so, I do not like posts with many questions.
The rules of this site/forum say "One and ONLY ONE question per post".
OK, three inter-connected questions are still possible, but 5 is definitely tooooooooooooo much.
|
|
|