SOLUTION: Two six-sided dice are rolled and the sum is recorded. Determine the probability of obtaining a sum greater than 8 and a sum less than 6.

               Part (a)


The full space of events is the set of all pairs  (i,j), where i and j are integer numbers from 1 to 6, inclusively.

This space consists of  6*6 = 36 elements, and each element/event has the probability of  .


Of them, the outcomes where the sum is greater than 8 are

    sum  9 :  (3,6), (4,5), (5,4), (6,3)            In all, 4 pairs.

    sum 10 :  (4,6), (5,5), (6,4)                   In all, 3 pairs.

    sum 11 :  (5,6), (6,5)                          In all, 2 pairs.

    sum 12 :  (6,6)                                 Only    1 pair.


Thus the number of events where the sum is greater thsan 8 is  4 + 3 + 2 + 1 = 10.


So, the probability to have the sum of two dice greater than 8 is 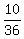  = .    ANSWER to (a)



               Part (b)


The full space of events is the set of all pairs  (i,j), where i and j are integer numbers from 1 to 6, inclusively.

This space consists of  6*6 = 36 elements, and each element/event has the probability of  .


Of them, the outcomes where the sum is less than 6 are

    sum  2 :  (1,1)                                 Only    1 pair.

    sum  3 :  (1,2), (2,1)                          In all, 2 pairs.

    sum  4 :  (1,3), (2,2), (3,1)                   In all, 3 pairs.

    sum  5 :  (1,4), (2,3), (3,2), (4,1)            In all, 4 pairs.


Thus the number of events where the sum is less than 6 is  1 + 2 + 3 + 4 = 10.


So, the probability to have the sum of two dice less than 6 is 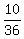  = .    ANSWER to (b)