The probability that a certain type of vacuum tube will shatter during a thermal shock test is 0.15.
The researches decide to test 80 vacuum tubes.
a) What is the mean number of vacuum tubes that will shatter?
b) What is the standard deviation of the number of vacuum tubes that will shatter?
c) Suppose that 17 of the 80 vacuum tubes shatter. Would you consider this unusual?
~~~~~~~~~~~~~~~~~~~~
Obvioulsly, the test is a binomial experiment.
(a) For binomial distribution, the mean is m = n*p = 80*0.15 = 12.
It is the ANSWER to (a).
(b) The standard deviation is s = 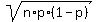 =
= 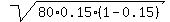 = 3.194 (rounded).
It is the ANSWER to (b).
(c) For (c), calculate the probability of this outcome. Use the standard formula for binomial distribution probability
P =
= 3.194 (rounded).
It is the ANSWER to (b).
(c) For (c), calculate the probability of this outcome. Use the standard formula for binomial distribution probability
P = 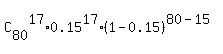 =
= 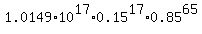 = 0.02583 (rounded).
So, this probability is quite small.
Notice that 17 is about 2 standard deviations of 3.1 (each) from the mean of 12, so, it confirms that such event
happens quite rare.
= 0.02583 (rounded).
So, this probability is quite small.
Notice that 17 is about 2 standard deviations of 3.1 (each) from the mean of 12, so, it confirms that such event
happens quite rare.
Solved.