Question 1205726: Two students agreed to meet at the Library between 6 pm and 7 pm. They also agree that the student arriving first will wait for a maximum of 25 minutes. What is the probability that they will meet, if they arrive at the Library between 6 pm and 7 pm randomly (uniform random distribution)?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two students agreed to meet at the Library between 6 pm and 7 pm.
They also agree that the student arriving first will wait for a maximum of 25 minutes.
What is the probability that they will meet, if they arrive at the Library between
6 pm and 7 pm randomly (uniform random distribution)?
~~~~~~~~~~~~~~~~
The space of events is the square in the coordinate plane (x,y), where x is the time when one student arrived
and y is the time when the other student arrived.
Since x and y are both between 6 pm a 7 pm, you may think that this square is of 60 units (minutes) side,
considering MINUTES between 6 pm and 7 pm for each event.
The set of points (x,y) (=the time moments x and y) where/(=when) they definitely will meet each other,
is the strip |x-y| <= 25.
It is the strip along the diagonal of the square.
So, you need to find the ratio of this strip area to the area 60x60 = 3600 of the entire square.
The area of the strip is the area of the square MINUS the area of the two triangles,
one of which is above the strip and the other is below the strip.
It is clear that each of these two triangles is isosceles right angled triangle with the leg size of 60-25 = 35 minutes.
Hence, the combined area of these two triangles is 35*35 = 1225 square units.
Then the area of the strip is 3600 - 1225 = 2375 square units.
From here, the probability under the question is  = = 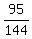 = 0.65972 (rounded). = 0.65972 (rounded).
Solved.
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Picture the diagram as described in the response from tutor @ikleyn.
Then here is a different way you can do the calculations to find the answer to the problem.
Note that the two isosceles right triangles representing the combinations of times when the two students do NOT meet have legs of "length" 35 minutes, or 7/12 of an hour.
Those two triangles put together form a square with side length 7/12 of an hour, so the area of those two triangles together is (7/12)^2 = 49/144 of the total area of the square.
Then the area of the square representing the combinations of times when the two students WILL meet is (144-49)/144 = 95/144 of the total area of the square. So
ANSWER: The probability that they will meet is 95/144
|
|
|