Question 1205344: If the sample mean is 8, the hypothesized population mean is 4, and the population standard deviation is 2, compute the test value need for the z test.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sample mean is 8.
population mean is assumed to be equal to 4.
population standard deviation is assumed to be equal to 2.
you don't have the sample size.
that's required if you are looking for the z-score associated with the mean of the sample.
you also need to used standard error rather than the standard deiation because that's required when you are looking for the z-score of the mean of a sample of specified size.
for example:
if the sample size is 100, then standard error = 2/sqrt(100) = .2
z = (x-m)/s becomes z = (8-4)/.2 = 4/.2 = 20.
if the sample size is 16, then standard error = 2/sqrt(16) = 2/4 = .5
z = (x-m)/s becomes z = (8-4)/.5 = 4/.5 = 8.
for a given standard deviation, the z-score is totally dependent on the sample size because the standard error is equal to the standard deviation divided by the square root of the sample size.
if you are taking about an individual sample, rather than the mean of a sample of specified size, then the standard deviation is used.
in this case, the formula of z = (x-m)/s becomes z = (8-4)/2 = 4/2 = 2.
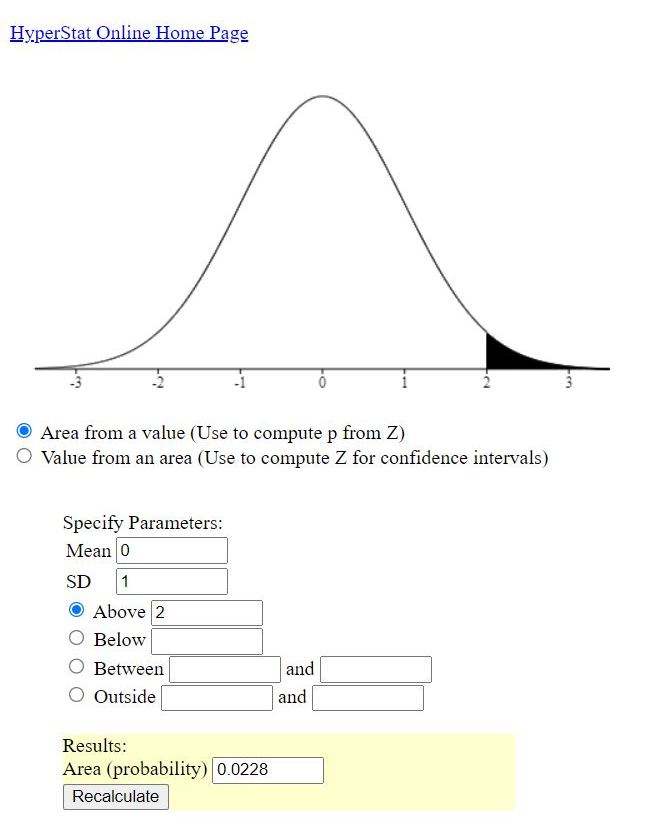
your test z-score is 2.
you then look for the area to the right of a z-score of 2 which will be equal to .02275 = 2.275%.
your test statistic is z = 2 and your p-value is equal to .02275.
.02275 is the proportion of the area under the normal distribution curve to the right of a z-score of 2.
on a graph, that looks like this.
|
|
|