SOLUTION: A deck of cards is shuffled well. The cards are dealt one-by-one until the two of hearts appears. Find the probability that exactly one king, queen, and jack appear before the two

Click here to see ALL problems on Probability-and-statistics

Question 1205065: A deck of cards is shuffled well. The cards are dealt one-by-one until the two of hearts appears. Find the probability that exactly one king, queen, and jack appear before the two of hearts.
a) 1/11 b) 1/22 c) 1/33 d) 1/44
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

It's the probability that a king, a queen, a jack, and the 2 of hearts come before the other 3 kings, the other 3 queens, and the other 3 jacks. We are only concerned with the following 13 cards. K, Q, J, 2 of hearts, K, K, K, Q, Q, Q, J, J, J The other 39 cards can go anywhere. We can choose the one king to come before the 2 of hearts 4 ways. We can choose the one queen to come before the 2 of hearts 4 ways. We can choose the one jack to come before the 2 of hearts 4 ways. Those 3 cards can be ordered 3! = 6 ways The 3 Kings, 3 queens, and 3 jacks that come after the 2 of hearts can be ordered any of 9! ways. The number of ways those 13 cards can come in the deck is 13! 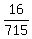So the desired probability is that simplifies to or about 0.022 I disagree with all your choices. Edwin

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
A deck of cards is shuffled well. The cards are dealt one-by-one until the two of hearts appears.
Find the probability that exactly one king, queen, and jack appear before the two of hearts.
a) 1/11 b) 1/22 c) 1/33 d) 1/44
~~~~~~~~~~~~~~~~~~~~~~~~

        As the problem is worded, it is AMBIGOUS.
        To avoid ambiguity, it should be re-formulated this way:

                Find the probability that exactly one king, queen, and jack appear
                 before the two of hearts.

        Agree that these are two different formulations describing two completely different situations.

The probability that 1-st dealt card is a king is . The probability that 2-nd dealt card is a queen is . The probability that 3-rd dealt card is a jack is . The probability that first three dealt cards are a king, a queen and a jack in any order is = . The probability that the next dealt card is the two of heard is . So, the probability to have four first cards as described is = = = = = 5.91006E-05. ANSWER There is nothing in common with your list of possible answers.

Solved.