Question 1204254: If the integers m and n are chosen at random from 1 to 100, then what is the probability that a number of the form 7^n+7^m is divisible by 5
a. 1/4 b. 1/2 c. 1/8 d. 1/3
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let  , then we observe that , then we observe that 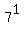 , , , , and and  ends in ends in  , , , , and and  respectively. respectively.
Thus, 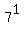 ends in ends in  , , , , and and  according as it is of the form according as it is of the form 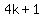 , , 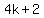 , , 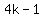 and and 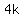 respectively. respectively.
If  is the sample space, then is the sample space, then 
 is divisible by is divisible by  , if: , if:
(1)  is of the form is of the form 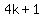 and and  is of the form is of the form 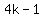 or or
(2)  is of the form is of the form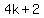 and and  is of the form is of the form 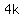 or or
(3)  is of the form is of the form 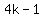 and and  is of the form is of the form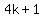 or or
(4)  is of the form is of the form 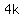 and and  is of the form is of the form 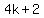
So, number of favorable ordered pairs ( , , )= )=
Required probability = 
answer:
.
a. 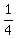
Answer by ikleyn(52925)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The content of the @MathLover1 post is copy-pasted without reference from this web-page
https://www.toppr.com/ask/en-us/question/if-the-integers-m-and-n-are-chosen-at-random/
|
|
|