Question 1204192: The probability that a certain machine turns out a defective item is 0.05. Find the
probability that in a run of 75 items, at least two are defective.
a.)0.8944 b.)0.08425 c.) 0.1056 d.) 0.8359 e.) 0.9158
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Answer: 0.8944 (choice A)
Explanation
We have a binomial probability distribution because of these reasons:- There are two options: the item is defective or it isn't.
- Each item has the same chance of being defective (5% chance)
- Each item is independent of one another.
Binomial probability distribution formula
B(x) = (nCx)*(p^x)*(1-p)^(n-x)
The nCx refers to the nCr combination formula.
n = 75 items total = sample size
p = 0.05 = probability of a defective item
x = values chosen from the set {0,1,2,3,...,74,75}
Use the binomial formula to compute B(0), which is the probability of getting 0 defective items in a batch of 75.
B(x) = (nCx)*(p^x)*(1-p)^(n-x)
B(0) = (75C0)*(0.05^0)*(1-0.05)^(75-0)
B(0) = (1)*(0.05^0)*(1-0.05)^(75-0)
B(0) = 0.021344 approximately
Repeat for x = 1
B(x) = (nCx)*(p^x)*(1-p)^(n-x)
B(1) = (75C1)*(0.05^1)*(1-0.05)^(75-1)
B(1) = (75)*(0.05^1)*(1-0.05)^(75-1)
B(1) = 0.084252 approximately
B(0)+B(1) = 0.021344+0.084252 = 0.105596 represents the probability of getting 0 defective items or 1 defective item.
The probability of getting 2 or more defective items is 1 - 0.105596 = 0.894404 which rounds to 0.8944
I'm using the idea that P(0 or 1 defects) + P(2 or more defects) = 1.
There's about an 89.44% chance of getting at least two defective items.
Another approach would be to use a calculator like this
https://www.gigacalculator.com/calculators/binomial-probability-calculator.php
Or you could use a TI83/TI84 calculator
https://www.statology.org/binomial-probabilities-ti-84-calculator/
The command you'll want is called BinomCDF.
More specifically you'll input 1-BinomCDF(75,0.05,1)
Or you could use the BinomDist spreadsheet function.
The spreadsheet command is
=Round(1-BinomDist(1,75,0.05,1),4)
The template for BinomDist is:
BinomDist(X,N,P,C)
where
X = number of successes
N = sample size
P = probability of success
C = either 0 or 1 depending if you want a PDF or CDF
Do not forget about the equal sign up front when typing in =Round(1-BinomDist(1,75,0.05,1),4) or the command won't execute.
Computing BinomDist(1,75,0.05,1) will produce the value B(0)+B(1) = 0.105596 that we found earlier.
Then we subtract it from 1 to get the value of B(2)+B(3)+...+B(74)+B(75) = 0.8944
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
At least 2 defective --> not either 0 or 1 defective.
P(0 defective) = 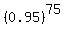 = .0213437 to several decimal places
P(1 defective) =  = .0842516
P(0 or 1 defective) = .0213437 + .0842516 = .1055953
P(at least 2 defective) = 1-.1055953 = .8944047
ANSWER: a) 0.8944
|
|
|
