Question 1204187: Suppose a study of the faculty at U.S. medical schools revealed that 33% of the faculty were women and 67% were men. Of the female faculty, 33% were full/associate professors, 49% were assistant professors, and 18% were instructors. Of the male faculty, 51% were full/associate professors, 36% were assistant professors, and 13% were instructors. If a faculty member at a U.S. medical school selected at random held the rank of full/associate professor, what is the probability that the faculty member was female? (Round your answer to two decimal places.)
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
Suppose a study of the faculty at U.S. medical schools revealed that 33% of the faculty were women and 67% were men.
Of the female faculty, 33% were full/associate professors, 49% were assistant professors, and 18% were instructors.
Of the male faculty, 51% were full/associate professors, 36% were assistant professors, and 13% were instructors.
If a faculty member at a U.S. medical school selected at random held the rank of full/associate professor,
what is the probability that the faculty member was female? (Round your answer to two decimal places.)
~~~~~~~~~~~~~~~~~~~~~~
The probability under the problem's question is the conditional probability.
So, this probability is the ratio, where the denominator is the number of full or associate professors
independently of the gender, while the numerator is the number of full or associate professors among women.
Based on it, the numerator is 0.33*0.33; the denominator is 0.33*0.33 + 0.67*0.51.
So, we write
P = 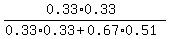 = 0.24 (rounded as requested). ANSWER
Solved.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
It's not necessary to make this chart for this one problem, but you
could have been given a number of probability questions instead of
just this one. Also making the complete chart makes it easier to
understand what's going on.
Female(33%) Male(67%)
Full/Asso.| 33% of 33% = 10.89% | 51% of 67% = 34.17%
Asst. | 49% of 33% = 16.17% | 36% of 67% = 24.12%
Inst. | 18% of 33% = 5.94% | 13% of 67% = 8.71%
If a faculty member at a U.S. medical school selected at random held
the rank of full/associate professor, what is the probability that the
faculty member was female?
P(Female | Full/Asso.) = P(Female AND Full/Asso.)/P(Full/Asso.) =
10.89%/(10.89%+34.17%) = 10.89%/45.06% = 0.241677763 which rounds to 0.24
Edwin
|
|
|
